Hopfield Neural Network (HNN) is a neural network with cyclic and recursive characteristics, combined with storage and binary systems. Invented by John Hopfield in 1982. For a Hopfield neural network, the key is to determine its weight under stable conditions . Hopfield neural networks are divided into discrete and continuous types. The main difference lies in the activation function.
The Hopfield Neural Network (HNN) provides a model that simulates human memory. It has a wide range of applications in artificial intelligence, such as machine learning, associative memory, pattern recognition, optimized calculation, VLSI and parallel realization of optical devices.
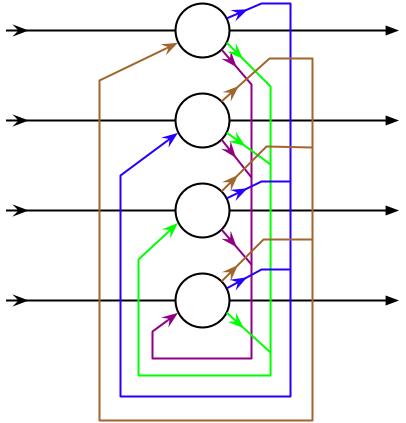
Network Structure
The HopField network is a cyclic neural network with feedback connections from output to input. After the signal is input, the state of the neuron will continue to change over time, and finally converge or periodically oscillate.
Suppose there are a total of N neurons, x_i is the input of the i-th neuron, w_{ij} is the weight between neuron i and j , θ_i is the threshold of the i-th neuron, if the i-th neuron is in the state y(i, t) at time t then we have the following recurrence formula:
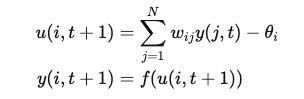
For simplicity, we consider a discrete HopField network, that is, f(x) is the sign function.
We introduce the concept of energy and define the increment of energy as:
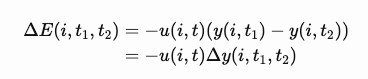
And,
As long as the state y of neuron i changes whether from 1 to -1 or from -1 to 1, the change value in energy Δ E will be negative. When the HopField network reaches stability, the energy function is minimal.
We define the energy of neuron i at time t as:
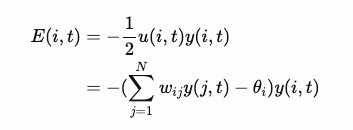
The total energy is:
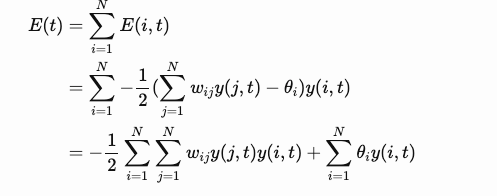
Example of Hopfield network status change
John Hopfield found that if the network connection is symmetric (wij=wji) and neurons have no self-feedback (wii=0), the network has a global energy function, and the correct network update rules make this energy function converge to a minimum. The update rules are:
Let’s use a specific example to illustrate that the neurons of the Hopfield network start from a random state, update one neuron at a time in a serialized manner, and finally reach a state of energy minimum.
In the initial state, only three neurons are activated and the total energy is -7.
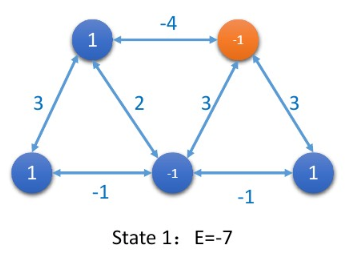
After updating 5 neurons, the total energy of the network reaches a minimum, and the network is in a stable state.
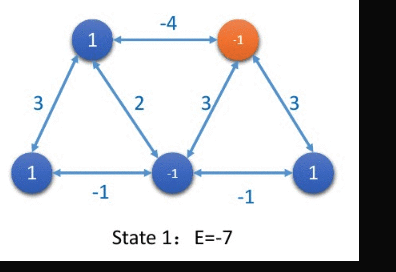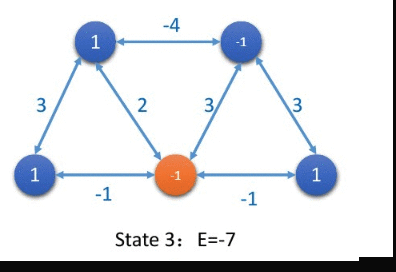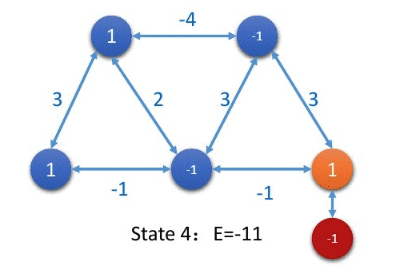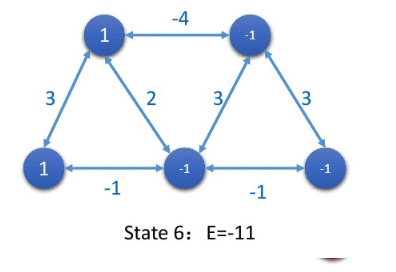
In addition to updating the status of each node in the sequence of serialization, the convergence can also be updated in a synchronous manner .
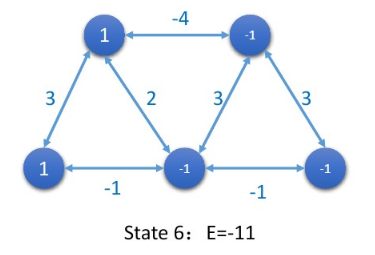
The final stable state of the network is called an attractor.
Learning rules
There are many learning methods, the most common is Hebb learning rule.
To learn a pattern p=[p_1,…,p_n] where pij=-/+1 .
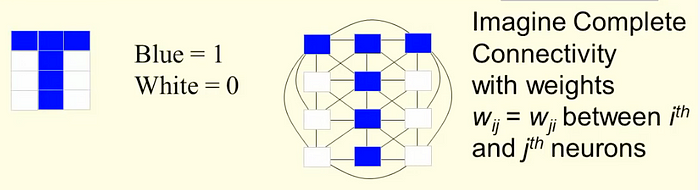
Given n interconnected neurons, the learning process regulation principle is that if two neurons i and j are excited at the same time, then the connection between them should be strengthened :
Where α is the learning rate and I is n x n identity matrix.
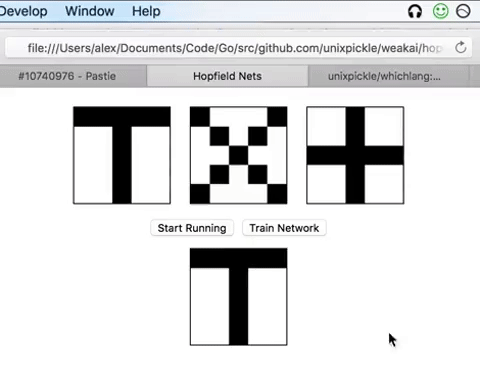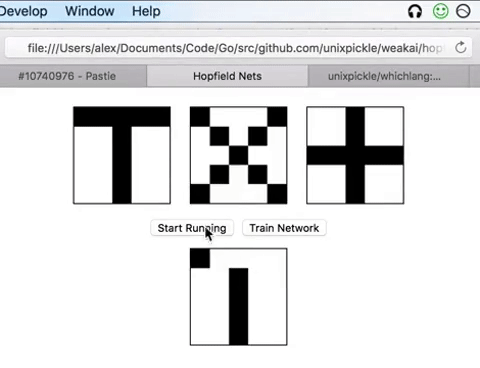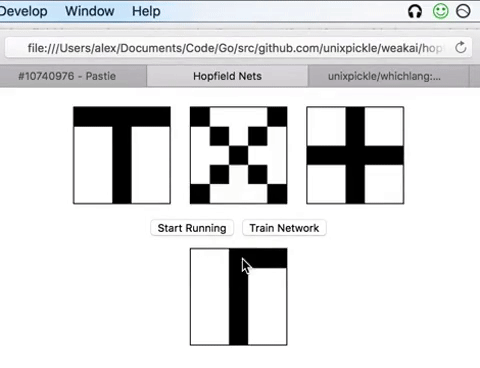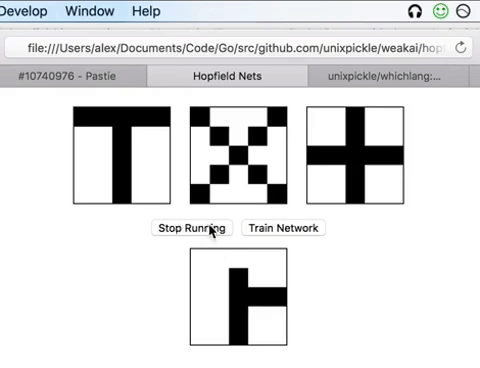
Pattern Recognition
Simulation begins with
Select neuron i at random and update via
This article has been published from the source link without modifications to the text. Only the headline has been changed.