Tutorial on Key Concepts in Calculus

In this graphical representation of the object’s movement, the rate of change is represented by the slope of the line, or its gradient. Since the line can be seen to rise 2 units for each single unit that it runs to the right, then its rate of change, or its slope, is equal to 2.

Rates and slopes have a simple connection. The previous rate examples can be graphed on an x-y coordinate system, where each rate appears as a slope.

Page 38, Calculus Essentials for Dummies, 2019.

Tying everything together, we see that:

rate of change = 𝛿y / 𝛿x = rise / run = slope

If we had to consider two particular points, P₁ = (2, 4) and P₂ = (8, 16), on this straight line, we may confirm the slope to be equal to:

slope = 𝛿y / 𝛿x = (y₂ – y₁) / (x₂ – x₁) = (16 – 4) / (8 – 2) = 2

For this particular example, the rate of change, represented by the slope, is positive since the direction of the line is increasing rightwards. However, the rate of change can also be negative if the direction of the line decreases, which means that the value of y would be decreasing as the value of x increases. Furthermore, when the value of y remains constant as x increases, we would say that we have zero rate of change. If, otherwise, the value of x remains constant as y increases, we would consider the range of change to be infinite, because the slope of a vertical line is considered undefined.

So far, we have considered the simplest example of having a straight line, and hence a linear function, with an unchanging slope. Nonetheless, not all functions are this simple, and if they were, there would be no need for calculus.

Calculus is the mathematics of change, so now is a good time to move on to parabolas, curves with changing slopes.

Page 39, Calculus Essentials for Dummies, 2019.

Let us consider a simple non-linear function, a parabola:

y = (1 / 4) x²

In contrast to the constant slope that characterises a straight line, we may notice how this parabola becomes steeper and steeper as we move rightwards.

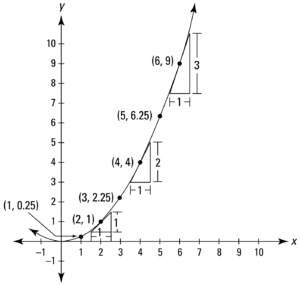
Line Plot of a Parabola Taken from Calculus Essentials For Dummies

Recall that the method of calculus allows us to analyse a curved shape by cutting it into many infinitesimal straight pieces arranged alongside one another. If we had to consider one of such pieces at some particular point, P, on the curved shape of the parabola, we see that we find ourselves calculating again the rate of change as the slope of a straight line. It is important to keep in mind that the rate of change on a parabola depends on the particular point, P, that we happened to consider in the first place.

For example, if we had to consider the straight line that passes through point, P = (2, 1), we find that the rate of change at this point on the parabola is:

rate of change = 𝛿y / 𝛿x = 1 / 1 = 1

If we had to consider a different point on the same parabola, at P = (6, 9), we find that the rate of change at this point is equal to:

rate of change = 𝛿y / 𝛿x = 3 / 1 = 3

The straight line that touches the curve as some particular point, P, is known as the tangent line, whereas the process of calculating the rate of change of a function is also known as finding its derivative.

A derivative is simply a measure of how much one thing changes compared to another — and that’s a rate.

Page 37, Calculus Essentials for Dummies, 2019.

While we have considered a simple parabola for this example, we may similarly use calculus to analyse more complicated non-linear functions. The concept of computing the instantaneous rate of change at different tangential points on the curve remains the same.

We meet one such example when we come to train a neural network using the gradient descent algorithm. As the optimization algorithm, gradient descent iteratively descends an error function towards its global minimum, each time updating the neural network weights to model better the training data. The error function is, typically, non-linear and can contain many local minima and saddle points. In order to find its way downhill, the gradient descent algorithm computes the instantaneous slope at different points on the error function, until it reaches a point at which the error is lowest and the rate of change is zero. 

The Importance of Measuring the Rate of Change

We have, thus far, considered the rate of change per unit on the x–y coordinate system.

But a rate can be anything per anything.

Page 38, Calculus Essentials for Dummies, 2019.

Within the context of training a neural network, for instance, we have seen that the error gradient is computed as the change in error with respect to a specific weight in the neural network. 

There are many different fields in which the measurement of the rate of change is an important concept too. A few examples are:

• In physics, speed is computed as the change in position per unit time.
• In signal digitisation, sampling rate is computed as the number of signal samples per second.
• In computing, bit rate is the number of bits the computer processes per unit time.
• In finance, exchange rate refers to the value of one currency with respect to another.

In either case, every rate is a derivative, and every derivative is a rate.

Page 38, Calculus Essentials for Dummies, 2019.

Summary

In this tutorial, you discovered the rate of change as one of the key concepts in calculus, and the importance of measuring it.

Specifically, you learned:

• The measurement of the rate of change is an integral concept in differential calculus that allows us to find the relationship of one changing variable with respect to another.
• This is an important concept that can be applied to many fields, one of which is machine learning.

This article has been published from the source link without modifications to the text. Only the headline has been changed.

Source link