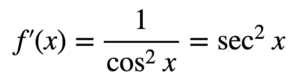Optimization, as one of the core processes in many machine learning algorithms, relies on the use of derivatives in order to decide in which manner to update a model’s parameter values, to maximize or minimize an objective function.
This tutorial will continue exploring the different techniques by which we can find the derivatives of functions. In particular, we will be exploring the power, product and quotient rules, which we can use to arrive to the derivatives of functions faster than if we had to find every derivative from first principles. Hence, for functions that are especially challenging, keeping such rules at hand to find their derivatives will become increasingly important.
In this tutorial, you will discover the power, product and quotient rules to find the derivative of functions.
After completing this tutorial, you will know:
- The power rule to follow when finding the derivative of a variable base, raised to a fixed power.
- How the product rule allows us to find the derivative of a function that is defined as the product of another two (or more) functions.
- How the quotient rule allows us to find the derivative of a function that is the ratio of two differentiable functions.
Let’s get started.
Tutorial Overview
This tutorial is divided into three parts; they are:
- The Power Rule
- The Product Rule
- The Quotient Rule
The Power Rule
If we have a variable base raised to a fixed power, the rule to follow in order to find its derivative is to bring down the power in front of the variable base, and then subtract the power by 1.
For example, if we have the function, f(x) = x2, of which we would like to find the derivative, we first bring down 2 in front of x and then reduce the power by 1:
f(x) = x2
f’(x) = 2x
For the purpose of understanding better where this rule comes from, let’s take the longer route and find the derivative of f(x) by starting from the definition of a derivative:
Here, we substitute for f(x) = x2 and then proceed to simplify the expression:
As h approaches a value of 0, then this limit approaches 2x, which tallies with the result that we have obtained earlier using the power rule.
If applied to f(x) = x, the power rule give us a value of 1. That is because, when we bring a value of 1 in front of x, and then subtract the power by 1, what we are left with is a value of 0 in the exponent. Since, x0 = 1, then f’(x) = (1) (x0)= 1.
The best way to understand this derivative is to realize that f(x) = x is a line that fits the form y = mx + b because f(x) = x is the same as f(x) = 1x + 0 (or y = 1x + 0). The slope (m) of this line is 1, so the derivative equals 1. Or you can just memorize that the derivative of x is 1. But if you forget both of these ideas, you can always use the power rule.
Page 131, Calculus for Dummies, 2016.
The power rule can be applied to any power, be it positive, negative, or a fraction. We can also apply it to radical functions by first expressing their exponent (or power) as a fraction:
f(x) = √x = x1/2
f’(x) = (1 / 2) x-1/2
The Product Rule
Suppose that we now have a function, f(x), of which we would like to find the derivative, which is the product of another two functions, u(x) = 2x2 and v(x) = x3:
f(x) = u(x) v(x) = (2x2) (x3)
In order to investigate how to go about finding the derivative of f(x), let’s first start with finding the derivative of the product of u(x) and v(x) directly:
(u(x) v(x))’ = ((2x2) (x3))’ = (2x5)’ = 10x4
Now let’s investigate what happens if we, otherwise, had to compute the derivatives of the functions separately first and then multiply them afterwards:
u’(x) v’(x) = (2x2)’ (x3)’ = (4x) (3x2) = 12x3
It is clear that the second result does not tally with the first one, and that is because we have not applied the product rule.
The product rule tells us that the derivative of the product of two functions can be found as:
f’(x) = u’(x) v(x) + u(x) v’(x)
We can arrive at the product rule if we our work our way through by applying the properties of limits, starting again with the definition of a derivative:
We know that f(x) = u(x) v(x) and, hence, we can substitute for f(x) and f(x + h):
At this stage, our aim is to factorise the numerator into several limits that can, then, be evaluated separately. For this purpose, the subtraction of terms, u(x) v(x + h) – u(x) v(x + h), shall be introduced into the numerator. Its introduction does not change the definition of f’(x) that we have just obtained, but it will help us factorise the numerator:
The resulting expression appears complicated, however, if we take a closer look we realize that we have common terms that can be factored out:
The expression can be simplified further by applying the limit laws that let us separate the sums and products into separate limits:
The solution to our problem has now become clearer. We can see that the first and last terms in the simplified expression correspond to the definition of the derivative of u(x) and v(x), which we can denote by u(x)’ and v(x)’, respectively. The second term approaches the continuous and differentiable function, v(x), as h approaches 0, whereas the third term is u(x).
Hence, we arrive again at the product rule:
f’(x) = u’(x) v(x) + u(x) v’(x)
With this new tool in hand, let’s reconsider finding f’(x) when u(x) = 2x2 and v(x) = x3:
f’(x) = u’(x) v(x) + u(x) v’(x)
f’(x) = (4x) (x3) + (2x2) (3x2) = 4x4 + 6x4 = 10x4
The resulting derivative now correctly matches the derivative of the product, (u(x) v(x))’, that we have obtained earlier.
This was a fairly simple example that we could have computed directly in the first place. However, we might have more complex problems involving power that cannot be multiplied directly, to which we can easily apply the product rule. For example:
f(x) = x2 sin x
f’(x) = (x2)’ (sin x) + (x2) (sin x)’ = 2x sin x + x2 cos x
We can even extend the product rule to more than two functions. For example, say f(x) is now defined as the product of three functions, u(x), v(x) and w(x):
f(x) = u(x) v(x) w(x)
We can apply the product rule as follows:
f’(x) = u’(x) v(x) w(x) + u(x) v’(x) w(x) + u(x) v(x) w’(x)
The Quotient Rule
Similarly, the quotient rule tells us how to find the derivative of a function, f(x), that is the ratio of two differentiable functions, u(x) and v(x):
We can derive the quotient rule from first principles as we have done for the product rule, that is by starting off with the definition of a derivative and applying the properties of limits. Or we can take a shortcut and derive the quotient rule using the product rule itself. Let’s take this route this time around:
We can apply the product rule on u(x) to obtain:
u’(x) = f’(x) v(x) + f(x) v’(x)
Solving back for f’(x) gives us:
One final step substitutes for f(x) to arrive to the quotient rule:
We had seen how to find the derivative of the sine and cosine functions. Using the quotient rule, we can now find the derivative of the tangent function too:
f(x) = tan x = sin x / cos x
Applying the quotient rule and simplifying the resulting expression:
From the Pythagorean identity in trigonometry, we know that cos2x + sin2x = 1, hence:
Therefore, using the quotient rule, we have easily found that the derivative of tangent is the squared secant function.
Summary
In this tutorial, you discovered how to apply the power, product and quotient rules to find the derivative of functions.
Specifically, you learned:
- The power rule to follow when finding the derivative of a variable base, raised to a fixed power.
- How the product rule allows us to find the derivative of a function that is defined as the product of another two (or more) functions.
- How the quotient rule allows us to find the derivative of a function that is the ratio of two differentiable functions.
This article has been published from the source link without modifications to the text. Only the headline has been changed.
Source link