- Mini-max algorithm is a recursive or backtracking algorithm which is used in decision-making and game theory. It provides an optimal move for the player assuming that opponent is also playing optimally.
- Mini-Max algorithm uses recursion to search through the game-tree.
- Min-Max algorithm is mostly used for game playing in AI. Such as Chess, Checkers, tic-tac-toe, go, and various tow-players game. This Algorithm computes the minimax decision for the current state.
- In this algorithm two players play the game, one is called MAX and other is called MIN.
- Both the players fight it as the opponent player gets the minimum benefit while they get the maximum benefit.
- Both Players of the game are opponent of each other, where MAX will select the maximized value and MIN will select the minimized value.
- The minimax algorithm performs a depth-first search algorithm for the exploration of the complete game tree.
- The minimax algorithm proceeds all the way down to the terminal node of the tree, then backtrack the tree as the recursion.
Pseudo-code for MinMax Algorithm:
-
function minimax(node, depth, maximizingPlayer) is
-
if depth ==0 or node is a terminal node then
-
return static evaluation of node
-
if MaximizingPlayer then // for Maximizer Player
-
maxEva= -infinity
-
for each child of node do
-
eva= minimax(child, depth-1, false)
-
maxEva= max(maxEva,eva) //gives Maximum of the values -
return maxEva -
else // for Minimizer player
-
minEva= +infinity
-
for each child of node do
-
eva= minimax(child, depth-1, true)
-
minEva= min(minEva, eva) //gives minimum of the values -
return minEva
Initial call:
Minimax(node, 3, true)
Working of Min-Max Algorithm:
- The working of the minimax algorithm can be easily described using an example. Below we have taken an example of game-tree which is representing the two-player game.
- In this example, there are two players one is called Maximizer and other is called Minimizer.
- Maximizer will try to get the Maximum possible score, and Minimizer will try to get the minimum possible score.
- This algorithm applies DFS, so in this game-tree, we have to go all the way through the leaves to reach the terminal nodes.
- At the terminal node, the terminal values are given so we will compare those value and backtrack the tree until the initial state occurs. Following are the main steps involved in solving the two-player game tree:
Step-1: In the first step, the algorithm generates the entire game-tree and apply the utility functions to get the utility values for the terminal states. In the below tree diagram, let’s take A is the initial state of the tree. Suppose maximizer takes first turn which has worst-case initial value =- infinity, and minimizer will take next turn which has worst-case initial value = +infinity.
Step 2: Now, first we find the utilities value for the Maximizer, its initial value is -∞, so we will compare each value in terminal state with initial value of Maximizer and determines the higher nodes values. It will find the maximum among the all.
- For node D max(-1,- -∞) => max(-1,4)= 4
- For Node E max(2, -∞) => max(2, 6)= 6
- For Node F max(-3, -∞) => max(-3,-5) = -3
- For node G max(0, -∞) = max(0, 7) = 7
Step 3: In the next step, it’s a turn for minimizer, so it will compare all nodes value with +∞, and will find the 3rd layer node values.
- For node B= min(4,6) = 4
- For node C= min (-3, 7) = -3
Step 4: Now it’s a turn for Maximizer, and it will again choose the maximum of all nodes value and find the maximum value for the root node. In this game tree, there are only 4 layers, hence we reach immediately to the root node, but in real games, there will be more than 4 layers.
- For node A max(4, -3)= 4
That was the complete workflow of the minimax two player game.
Properties of Mini-Max algorithm:
- Complete- Min-Max algorithm is Complete. It will definitely find a solution (if exist), in the finite search tree.
- Optimal- Min-Max algorithm is optimal if both opponents are playing optimally.
- Time complexity- As it performs DFS for the game-tree, so the time complexity of Min-Max algorithm is O(bm), where b is branching factor of the game-tree, and m is the maximum depth of the tree.
- Space Complexity- Space complexity of Mini-max algorithm is also similar to DFS which is O(bm).
Limitation of the minimax Algorithm:
The main drawback of the minimax algorithm is that it gets really slow for complex games such as Chess, go, etc. This type of games has a huge branching factor, and the player has lots of choices to decide. This limitation of the minimax algorithm can be improved from alpha-beta pruning which we have discussed in the next topic.
Alpha-Beta Pruning
- Alpha-beta pruning is a modified version of the minimax algorithm. It is an optimization technique for the minimax algorithm.
- As we have seen in the minimax search algorithm that the number of game states it has to examine are exponential in depth of the tree. Since we cannot eliminate the exponent, but we can cut it to half. Hence there is a technique by which without checking each node of the game tree we can compute the correct minimax decision, and this technique is called pruning. This involves two threshold parameter Alpha and beta for future expansion, so it is called alpha-beta pruning. It is also called as Alpha-Beta Algorithm.
- Alpha-beta pruning can be applied at any depth of a tree, and sometimes it not only prune the tree leaves but also entire sub-tree.
- The two-parameter can be defined as:
- Alpha: The best (highest-value) choice we have found so far at any point along the path of Maximizer. The initial value of alpha is -∞.
- Beta: The best (lowest-value) choice we have found so far at any point along the path of Minimizer. The initial value of beta is +∞.
- The Alpha-beta pruning to a standard minimax algorithm returns the same move as the standard algorithm does, but it removes all the nodes which are not really affecting the final decision but making algorithm slow. Hence by pruning these nodes, it makes the algorithm fast.
Condition for Alpha-beta pruning:
The main condition which required for alpha-beta pruning is:
-
α>=β
Key points about alpha-beta pruning:
- The Max player will only update the value of alpha.
- The Min player will only update the value of beta.
- While backtracking the tree, the node values will be passed to upper nodes instead of values of alpha and beta.
- We will only pass the alpha, beta values to the child nodes.
Pseudo-code for Alpha-beta Pruning:
-
function minimax(node, depth, alpha, beta, maximizingPlayer) is
-
if depth ==0 or node is a terminal node then
-
return static evaluation of node
-
if MaximizingPlayer then // for Maximizer Player
-
maxEva= -infinity
-
for each child of node do
-
eva= minimax(child, depth-1, alpha, beta, False) -
maxEva= max(maxEva, eva)
-
alpha= max(alpha, maxEva)
-
if beta<=alpha -
break -
return maxEva -
else // for Minimizer player
-
minEva= +infinity
-
for each child of node do
-
eva= minimax(child, depth-1, alpha, beta, true)
-
minEva= min(minEva, eva)
-
beta= min(beta, eva)
-
if beta<=alpha -
break -
return minEva
Working of Alpha-Beta Pruning:
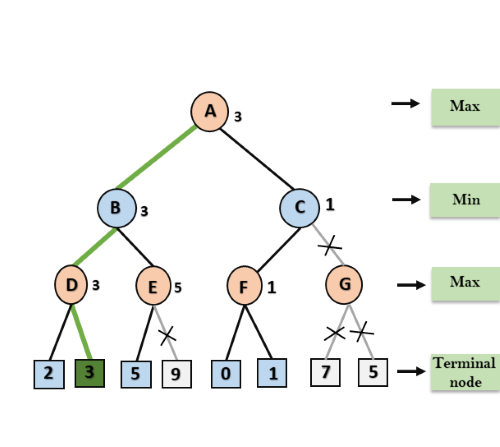
Let’s take an example of two-player search tree to understand the working of Alpha-beta pruning
Step 1: At the first step the, Max player will start first move from node A where α= -∞ and β= +∞, these value of alpha and beta passed down to node B where again α= -∞ and β= +∞, and Node B passes the same value to its child D.
Step 2: At Node D, the value of α will be calculated as its turn for Max. The value of α is compared with firstly 2 and then 3, and the max (2, 3) = 3 will be the value of α at node D and node value will also 3.
Step 3: Now algorithm backtrack to node B, where the value of β will change as this is a turn of Min, Now β= +∞, will compare with the available subsequent nodes value, i.e. min (∞, 3) = 3, hence at node B now α= -∞, and β= 3.
In the next step, algorithm traverse the next successor of Node B which is node E, and the values of α= -∞, and β= 3 will also be passed.
Step 4: At node E, Max will take its turn, and the value of alpha will change. The current value of alpha will be compared with 5, so max (-∞, 5) = 5, hence at node E α= 5 and β= 3, where α>=β, so the right successor of E will be pruned, and algorithm will not traverse it, and the value at node E will be 5.
Step 5: At next step, algorithm again backtrack the tree, from node B to node A. At node A, the value of alpha will be changed the maximum available value is 3 as max (-∞, 3)= 3, and β= +∞, these two values now passes to right successor of A which is Node C.
At node C, α=3 and β= +∞, and the same values will be passed on to node F.
Step 6: At node F, again the value of α will be compared with left child which is 0, and max(3,0)= 3, and then compared with right child which is 1, and max(3,1)= 3 still α remains 3, but the node value of F will become 1.
Step 7: Node F returns the node value 1 to node C, at C α= 3 and β= +∞, here the value of beta will be changed, it will compare with 1 so min (∞, 1) = 1. Now at C, α=3 and β= 1, and again it satisfies the condition α>=β, so the next child of C which is G will be pruned, and the algorithm will not compute the entire sub-tree G.
Step 8: C now returns the value of 1 to A here the best value for A is max (3, 1) = 3. Following is the final game tree which is the showing the nodes which are computed and nodes which has never computed. Hence the optimal value for the maximizer is 3 for this example.
Move Ordering in Alpha-Beta pruning:
The effectiveness of alpha-beta pruning is highly dependent on the order in which each node is examined. Move order is an important aspect of alpha-beta pruning.
It can be of two types:
- Worst ordering: In some cases, alpha-beta pruning algorithm does not prune any of the leaves of the tree, and works exactly as minimax algorithm. In this case, it also consumes more time because of alpha-beta factors, such a move of pruning is called worst ordering. In this case, the best move occurs on the right side of the tree. The time complexity for such an order is O(bm).
- Ideal ordering: The ideal ordering for alpha-beta pruning occurs when lots of pruning happens in the tree, and best moves occur at the left side of the tree. We apply DFS hence it first search left of the tree and go deep twice as minimax algorithm in the same amount of time. Complexity in ideal ordering is O(bm/2).
Rules to find good ordering:
Following are some rules to find good ordering in alpha-beta pruning:
- Occur the best move from the shallowest node.
- Order the nodes in the tree such that the best nodes are checked first.
- Use domain knowledge while finding the best move. Ex: for Chess, try order: captures first, then threats, then forward moves, backward moves.
- We can bookkeep the states, as there is a possibility that states may repeat.
This article has been published from the source link without modifications to the text. Only the headline has been changed.
Source link