Wallets
Wallets are containers for private keys, usually implemented as structured files or simple databases. Another method for making keys is deterministic key generation. Here you derive each new private key, using a one-way hash function from a previous private key, linking them in a sequence. As long as you can re-create that sequence, you only need the first key (known as a seed or master key) to generate them all. In this section we will examine the different methods of key generation and the wallet structures that are built around them.
Wallets contain keys, not coins. The coins are stored on the block‐ chain in the form of transaction-outputs (often noted as vout or txout). Each user has a wallet containing keys. Wallets are really key‐ chains containing pairs of private/public keys (See (to come)). Users sign transactions with the keys, thereby proving they own the trans‐ action outputs (their coins).
Non-Deterministic (Random) Wallets
In the first implementations of bitcoin clients, wallets were simply collections of ran‐ domly generated private keys. This type of wallet is called a Type-0 Non-Deterministic Wallets. For example, the Bitcoin Core Client pre-generates 100 random private keys when first started and generates more keys as needed, using each key only once. This type of wallet is nicknamed “Just a Bunch Of Keys”, or JBOK, and such wallets are being replaced with deterministic wallets because they are cumbersome to manage, backup and import. The disadvantage of random keys is that if you generate many of them you must keep copies of all of them, meaning that the wallet must be backed-up frequently. Each key must be backed-up, or the funds it controls are irrevocably lost if the wallet becomes inaccessible. This conflicts directly with the principle of avoiding address reuse, by using each bitcoin address for only one transaction. Address re-use reduces privacy by associating multiple transactions and addresses with each other. A Type-0 non-deterministic wallet is a poor choice of wallet, especially if you want to avoid address re-use as that means managing many keys, which creates the need for frequent backups. While the Bitcoin Core Client includes a wallet that is implemented as a Type-0 wallet, the use of this wallet is actively discouraged by developers of the Bitcoin Core.
Deterministic (Seeded) Wallets
Deterministic, or “seeded” wallets are wallets that contain private keys which are all derived from a common seed, through the use of a one-way hash function. The seed is a randomly generated number which is combined with other data, such as an index number or “chain code” to derive the private keys. In a deterministic wallet, the seed is sufficient to recover all the derived keys and therefore a single backup at creation time is sufficient. The seed is also sufficient for a wallet export or import, allowing for easy migration of all the user’s keys between different wallet implementations.
Mnemonic Code Words
Mnemonic codes are English word sequences that represent (encode) a random number used as a seed to derive a deterministic wallet. The sequence of words is sufficient to recreate the seed and from there re-create the wallet and all the derived keys. A wallet application that implements deterministic wallets with mnemonic code will show the user a sequence of 12-24 words when first creating a wallet. That sequence of words is the wallet backup and can be used to recover and re-create all the keys in the same or any compatible wallet application. Mnemonic code words make it easier for users to back up wallets, as they are easy to read and correctly transcribe, as compared to a random sequence of numbers.
Mnemonic codes are defined in Bitcoin Improvement Proposal 39 (see [bip0039]), currently in Draft status. Note that BIP0039 is a draft proposal and not a standard. Specifically, there is a different standard, with a different set of words used by the Elec‐ trum wallet and predating BIP0039. BIP0039 is used by the Trezor wallet and a few other wallets but is incompatible with Electrum’s implementation.
BIP0039 defines the creation of a mnemonic code and seed as a follows:
1. Create a random sequence (entropy) of 128 to 256 bits
2. Create a checksum of the random sequence by taking the first few bits of its SHA256 hash 3. Add the checksum to the end of the random sequence
4. Divide the sequence into sections of 11 bits, using those to index a dictionary of 2048 pre-defined words
5. Produce 12-24 words representing the mnemonic code
Table – Mnemonic Codes: Entropy and Word Length
| Entropy (bits) | Checksum (bits) | Entropy+Checksum | Word Length |
| 128 160 192 224 256 |
4 5 6 7 8 |
132 165 198 231 264 |
12 15 18 21 24 |
The mnemonic code represents 128 to 256 bits which are used to derive a longer (512 bit) seed through the use of the key-stretching function PBKDF2. The resulting seed is used to create a deterministic wallet and all of its derived keys.
Here are some examples of mnemonic codes and the seeds they produce:
Table – 128-bit entropy mnemonic code and resulting seed
entropy input 0c1e24e5917779d297e14d45f14e1a1a (128 bits) mnemonic army van defense carry jealous true garbage claim echo media make crunch (12 words) seed (512 bits) 3338a6d2ee71c7f28eb5b882159634cd46a898463e9d2d0980f8e80dfbba5b0fa0291e5fb88\ 8a599b44b93187be6ee3ab5fd3ead7dd646341b2cdb8d08d13bf7
Table – 256-bit entropy mnemonic code and resulting seed
entropyinput 2041546864449caff939d32d574753fe684d3c947c3346713dd8423e74abcf8c (256 bits) mnemonic (24 cakeappleborrow silkendorsefitness topdenialcoil riot stay wolf luggageoxygen faintmajoreditmeasure invite love trap field dilemma oblige words) seed (512 bits) 3972e432e99040f75ebe13a660110c3e29d131a2c808c7ee5f1631d0a977fcf473bee22\ fce540af281bf7cdeade0dd2c1c795bd02f1e4049e205a0158906c343
Hierarchical Deterministic Wallets (BIP0032/BIP0044)
Deterministic wallets were developed to make it easy to derive many keys from a single “seed”. The most advanced form of deterministic wallets is the Hierarchical Determin‐ istic Wallet or HD Wallet defined by the BIP0032 standard. Hierarchical deterministic wallets contain keys derived in a tree structure, such that a parent key can derive a sequence of children keys, each of which can derive a sequence of grandchildren keys and so on to an infinite depth. This tree structure is illustrated below:
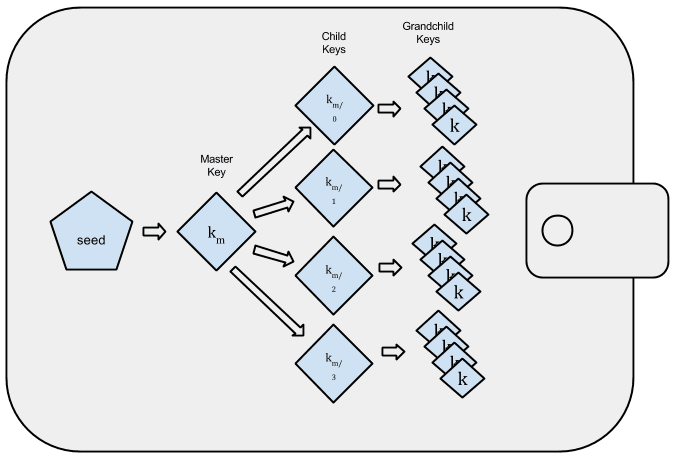
If you are implementing a bitcoin wallet, it should be built as an HD wallet following the BIP0032 and BIP0044 standards.
HD wallets offer two major advantages over random (non-deterministic) keys. First, the tree structure can be used to express additional organizational meaning, such as when a specific branch of sub-keys is used to receive incoming payments and a different branch is used to receive change from outgoing payments. Branches of keys can also be used in a corporate setting, allocating different branches to departments, subsidiaries, specific functions or accounting categories.
The second advantage of HD wallets is that users can create a sequence of public keys without having access to the corresponding private keys. This allows HD wallets to be used on an insecure server or in a receive-only capacity, issuing a different public key for each transaction. The public keys do not need to be pre-loaded or derived in advance, yet the server doesn’t have the private keys that can spend the funds.
HD wallet creation from a seed
HD wallets are created from a single root seed, which is a 128, 256 or 512 bit random number. Everything else in the HD wallet is deterministically derived from this root seed, which makes it possible to re-create the entire HD wallet from that seed in any compatible HD wallet. This makes it easy to backup, restore, export and import HD wallets containing thousands or even millions of keys by simply transferring only the root seed.
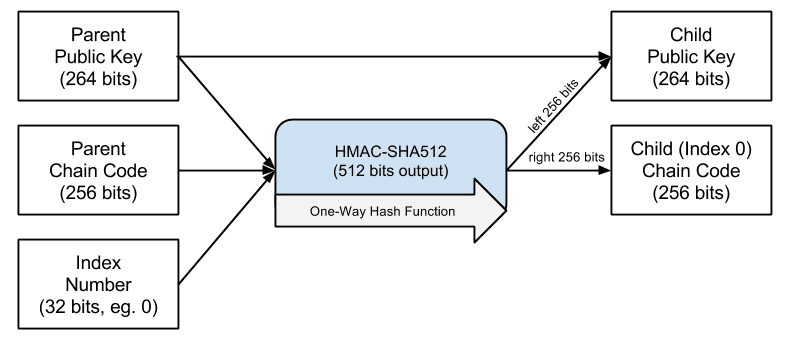
The process of creating the master keys and master chain code for an HD wallet is shown below:
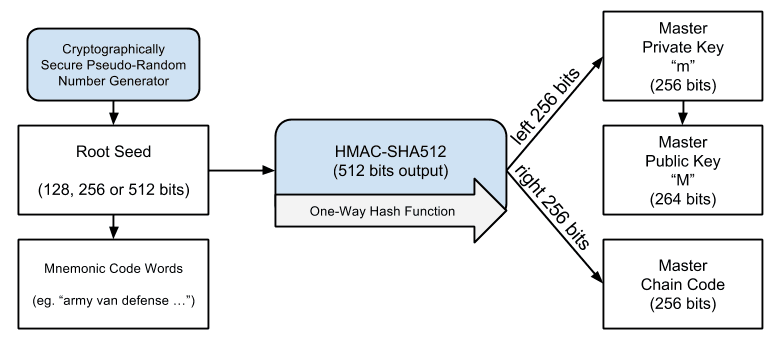
The root seed is input into the HMAC-SHA512 algorithm and the resulting hash is used to create a master private key (m) and a master chain code. The master private key (m) then generates a corresponding master public key (M), using the normal elliptic curve multiplication process m * G that we saw previously in this chapter. The chain code is used to introduce entropy in the function that creates child keys from parent keys, as we will see in the next section.
Private child key derivation
Hierarchical Deterministic wallets use a child key derivation (CKD) function to derive children keys from parent keys.
The child key derivation functions are based on one-way hash functions that combines:
• A parent private or public key (ECDSA uncompressed key)
• A seed called a chain code (256 bits)
• An index number (32 bits)
The chain code is used to introduce seemingly random data to the process, so that the index is not sufficient to derive other child keys. Thus, having a child key does not make it possible to find its siblings, unless you also have the chain code. The initial chain code seed (at the root of the tree) is made from random data, while subsequent chain codes are derived from each parent chain code.
These three items are combined and hashed to generate children keys, as follows:
The parent public key, chain code and the index number are combined and hashed with the HMAC-SHA512 algorithm to produce a 512 bit hash. The resulting hash is split into two halfs. The right-half 256 bits of the hash output become the chain code for the child. The left-half 256 bits of the hash and the index number are added to the parent private key to produce the child private key. In the diagram below, we see this illustrated with the index set to 0 to produce the 0’th (first by index) child of the parent.
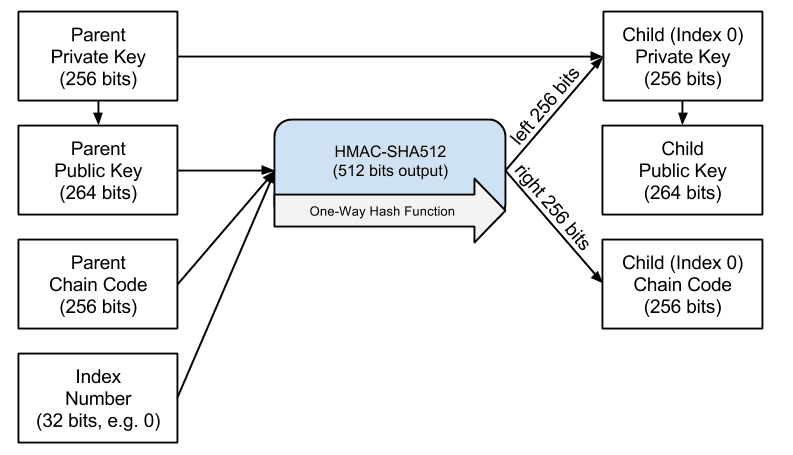
Changing the index allows us to extend the parent and create the other children in the sequence, e.g. Child 0, Child 1, Child 2 etc. Each parent key can have 2 billion children keys.
Repeating the process one level down the tree, each child can in turn become a parent and create its own children, in an infinite number of generations.
Using derived child keys
Child private keys are indistinguishable from non-deterministic (random) keys. Be‐ cause the derivation function is a one way function, the child key cannot be used to find the parent key. The child key can also not be used to find any siblings. If you have the nth child, you cannot find its siblings, such as the n-1 child or the n+1 child, or any other children that are part of the sequence. Only the parent key and chain code can derive all the children. Without the child chain code, the child key cannot be used to derive any grandchildren either. You need both the child private key and the child chain code to start a new branch and derive grandchildren.
So what can the child private key be used for on its own? It can be used to make a public key and a bitcoin address. Then, it can be used to sign transactions to spend anything paid to that address.
A child private key, the corresponding public key and the bitcoin address are all indistinguishable from keys and addresses created randomly. The fact that they are part of a sequence is not visible, outside of the HD wallet function that created them. Once created, they operate exactly as “normal” keys.
Extended keys
As we saw above, the key derivation function can be used to create children at any level of the tree, based on the three inputs: a key, a chain code and the index of the desired child. The two essential ingredients are the key and chain code and combined these are called an extended key. The term “extended key” could also be thought of as “extensible key” because such a key can be used to derive children.
Extended keys are stored and represented simply as the concatenation of the 256 bit key and 256 bit chain code into a 512 bit sequence. There are two types of extended keys: An extended private key is the combination of a private key and chain code and can be used to derive child private keys (and from them, child public keys). An extended public key is a public key and chain code, which can be used to create child public keys.
Think of an extended key as the root of a branch in the tree structure of the HD wallet. With the root of the branch, you can derive the rest of the branch. The extended private key can create a complete branch, whereas the extended public key can only create a branch of public keys.
An extended key consists of a private or public key and chain code. An extended key can create children generating its own branch in the tree structure. Sharing an extended key gives access to the entire branch.
Extended keys are encoded using Base58Check, to easily export and import between different BIP0032 compatible wallets. The Base58Check coding for extended keys uses a special version number that results in the prefix “xprv” and “xpub” when encoded in base 58 characters, to make them easily recognizable. Since the extended key is 512 or 513 bits, it is also much longer than other Base58Check encoded strings we have seen previously.
Here’s an example of an extended private key, encoded in Base58Check
xprv9tyUQV64JT5qs3RSTJkXCWKMyUgoQp7F3hA1xzG6ZGu6u6Q9VMNjGr67Lctvy5P8oyaYAL9CAWrUE9i6GoNMKUga5biW6Hx4tws2six3b9c
Here’s the corresponding extended public key, also encoded in Base58Check:
xpub67xpozcx8pe95XVuZLHXZeG6XWXHpGq6Qv5cmNfi7cS5mtjJ2tgypeQbBs2UAR6KECeeMVKZBPLrtJunSDMstweyLXhRgPxdp14sk9tJPW9
Public child key derivation
As mentioned above, a very useful characteristic of hierarchical deterministic wallets is the ability to derive public child keys from public parent keys, without having the private keys. This gives us two ways to derive a child public key: either from the child private key, or directly from the parent public key.
An extended public key can be used, therefore, to derive all of the public keys (and only the public keys) in that branch of the HD wallet structure.
This shortcut can be used to create very secure public-key-only deployments where a server or application has a copy of an extended public key and no private keys whatso‐ ever. That kind of deployment can produce an infinite number of public keys and bitcoin addresses but cannot spend any of the money sent to those addresses. Meanwhile, on another more secure server, the extended private key can derive all the corresponding private keys to sign transactions and spend the money.
One common application of this solution is to install an extended public key on a web server that serves an e-commerce application. The web server can use the public key derivation function to create a new bitcoin address for every transaction (e.g. for a customer shopping cart). The web server will not have any private keys that would be vulnerable to theft. Without HD wallets, the only way to do this is to generate thousands of bitcoin addresses on a separate secure server and then pre-load them on the ecommerce server. That approach is cumbersome and requires constant maintenance to ensure that the e-commerce server doesn’t “run out” of keys.
Another common application of this solution is for cold-storage or hardware wallets. In that scenario, the extended private key can be stored on a paper wallet or hardware device (such as a Trezor hardware wallet), while the extended public key can be kept online. The user can create “receive” addresses at will, while the private keys are safely stored offline. To spend the funds, they can use the extended private key on an offline signing bitcoin client or sign transactions on the hardware wallet device (e.g. Trezor).
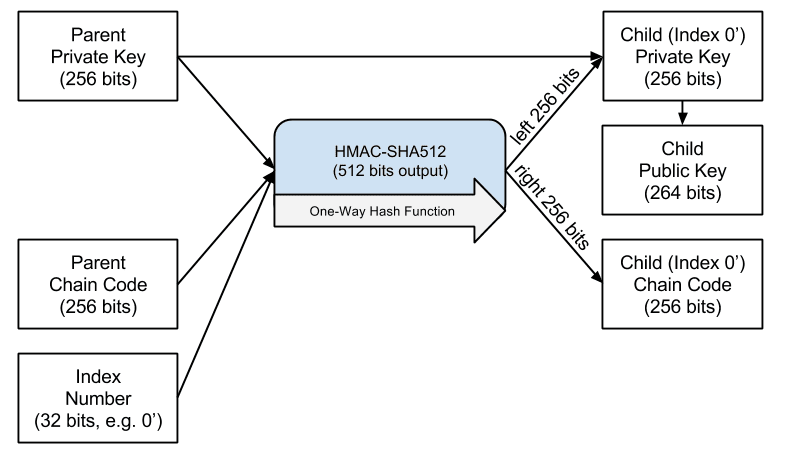
Hardened child key derivation
The ability to derive a branch of public keys from an extended public key is very useful, but it comes with a potential risk. Access to an extended public key does not give access to child private keys. However, because the extended public key contains the chain code, if a child private key is known, or somehow leaked, it can be used with the chain code to derive all the other child private keys. A single leaked child private key, together with a parent chain code, reveals all the private keys of all the children. Worse, the child private key together with a parent chain code can be used to deduce the parent private key.
key. To counter this risk, HD wallets use an alternative derivation function called hardened derivation, which “breaks” the relationship between parent public key and child chain code. The hardened derivation function uses the parent private key to derive the child chain code, instead of the parent public key. This creates a “firewall” in the parent/child sequence, with a chain code that cannot be used to compromise a parent or sibling private key. The hardened derivation function looks almost identical to the normal child private key derivation, except that the parent private key is used as input to the hash function, instead of the parent public key, as shown in the diagram below:
When the hardened private derivation function is used, the resulting child private key and chain code are completely different from what would result from the normal der‐ ivation function. The resulting “branch” of keys can be used to produce extended public keys which are not vulnerable, since the chain code they contain cannot be exploited to reveal any private keys. Hardened derivation is therefore used to create a “gap” in the tree above the level where extended public keys are used.
In simple terms, if you want to use the convenience of an extended public key to derive branches of public keys, without exposing yourself to the risk of a leaked chain code, you should derive it from a hardened parent, rather than a normal parent. As a best practice, the level-1 children of the master keys are always derived through the hardened derivation, to prevent compromise of the master keys.
Index numbers for normal and hardened derivation
The index number used in the derivation function is a 32-bit integer. To easily distin‐ guish between keys derived through the normal derivation function versus keys derived through hardened derivation, this index number is split into two ranges. Index numbers between 0 and 2^31-1 (0x0 to 0x7FFFFFFF) are used only for normal derivation. Index numbers between 2^31 and 2^32-1 (0x80000000 to 0xFFFFFFFF) are used only for hardened derivation. Therefore, if the index number is less than 2^31, that means the child is normal, whereas if the index number is equal or above 2^31, the child is hardened.
To make the index number easier to read and display, the index number for hardened children is displayed starting from zero, but with a prime symbol. The first normal child key is therefore displayed as 0, whereas the first hardened child (index 0x80000000) is displayed as 0’. In sequence then, the second hardened key would have index 0x80000001 and would be displayed as 1′, and so on. When you see an HD wallet index i’, that means 2^31+i.
HD wallet key identifier (path)
Keys in an HD wallet are identified using a “path” naming convention, with each level of the tree separated by a slash (/) character. Private keys derived from the master private key start with “m”. Public keys derived from the master public key start with “M”. There‐ fore, the first child private key of the master private key is m/0. The first child public key is M/0. The second grandchild of the first child is m/0/1 and so on.
The “ancestry” of a key is read from right to left, until you reach the master key from which it was derived. For example, identifier m/x/y/z describes the key which is the zth child of key m/x/y, which is the y-th child of key m/x, which is the x-th child of m.
Table 4-8. HD wallet path examples
m/0 The first (0) child private key from the master private key (m) m/0/0 The first grandchild private key of the first child (m/0) m/0'/0 The first normal grandchild of the first hardened child (m/0') m/1/0 The first grandchild private key of the second child (m/1) M/23/17/0/0 The first great-great-grandchild public key of the first great-grandchild of the 18th grandchild of the 24th child
Navigating the HD wallet tree structure
The HD wallet tree structure offers tremendous flexibility. Each parent extended key can have 4 billion children: 2 billion normal children and 2 billion hardened children. Each of those children can have another 4 billion children and so on. The tree can be as deep as you want, with an infinite number of generations. With all that flexibility, however, it becomes quite difficult to navigate this infinite tree. It is especially difficult to transfer HD wallets between implementations, because the possibilities for internal organization into branches and sub-branches are endless.
Two Bitcoin Improvement Proposals (BIPs) offer a solution to this complexity, by cre‐ ating some proposed standards for the structure of HD wallet trees. BIP0043 proposes the use of the first hardened child index as a special identifier that signifies the “purpose” of the tree structure. Based on BIP0043, an HD wallet should use only one level-1 branch of the tree, with the index number identifying the structure and namespace of the rest of the tree by defining its purpose. For example, an HD wallet using only branch m/i’/, is intended to signify a specific purpose and that purpose is identified by index number “i”.
Extending that specification, BIP0044 proposes a multi-account structure as “purpose” number 44′ under BIP0043. All HD wallets following the BIP0044 structure are iden‐ tified by the fact that they only used one branch of the tree: m/44’/.
BIP0044 specifies the structure as consisting of five pre-defined tree levels:
m / purpose' / coin_type' / account' / change / address_index
The first level “purpose” is always set to 44′. The second level “coin_type” specifies the type of crypto-currency coin, allowing for multi-currency HD wallets where each cur‐ rency has its own subtree under the second level. There are three currencies defined for now: Bitcoin is m/44’/0′, Bitcoin Testnet is m/44’/1’ and Litecoin is m/44’/2’
The third level of the tree is “account”, which allows users to subdivide their wallets into separate logical sub-accounts, for accounting or organizational purposes. For example, an HD wallet might contain two bitcoin “accounts”: m/44’/0’/0’ and m/44’/0’/1’. Each account is the root of its own sub-tree.
On the fourth level “change”, an HD wallet has two sub-trees, one for creating receiving addresses and one for creating change addresses. Note that whereas the previous levels used hardened derivation, this level uses normal derivation. This is to allow this level of the tree to export extended public keys for use in an non-secured environment. Usable addresses are derived by the HD wallet as children of the fourth level, making the fifth level of the tree the “address_index”. For example, the third receiving address for bitcoin payments in the primary account would be M/44’/0’/0’/0/2. Here are a few more exam‐ ples:
Table 4-9. BIP0044 HD wallet structure examples
M/44'/0'/0'/0/2 The third receiving public key for the primary bitcoin account M/44'/0'/3'/1/14 The fifteenth change-address public key for the fourth bitcoin account m/44'/2'/0'/0/1 The second private key in the Litecoin main account, for signing transactions
Experimenting with HD wallets using sx-tools
Using the command line tool sx, introduced in Chapter 3, you can experiment with generating and extending BIP0032 deterministic keys, as well as displaying them in different formats:
$ sx hd-seed > m # create a new master private key from a seed and store in file "m" $ cat m # show the master extended private key xprv9s21ZrQH143K38iQ9Y5p6qoB8C75TE71NfpyQPdfGvzghDt39DHPFpovvtWZaRgY5uPwV7RpEgHs7cvd\ gfiSjLjjbuGKGcjRyU7RGGSS8Xa $ cat m | sx hd-pub 0 # generate the M/0 extended public key xpub67xpozcx8pe95XVuZLHXZeG6XWXHpGq6Qv5cmNfi7cS5mtjJ2tgypeQbBs2UAR6KECeeMVKZBPLrtJun\ SDMstweyLXhRgPxdp14sk9tJPW9 $ cat m | sx hd-priv 0 # generate the m/0 extended private key xprv9tyUQV64JT5qs3RSTJkXCWKMyUgoQp7F3hA1xzG6ZGu6u6Q9VMNjGr67Lctvy5P8oyaYAL9CAWrUE9i6\ GoNMKUga5biW6Hx4tws2six3b9c $ cat m | sx hd-priv 0 | sx hd-to-wif # show the private key of m/0 as a WIF L1pbvV86crAGoDzqmgY85xURkz3c435Z9nirMt52UbnGjYMzKBUN $ cat m | sx hd-pub 0 | sx hd-to-address # show the bitcoin address of M/0 1CHCnCjgMNb6digimckNQ6TBVcTWBAmPHK $ cat m | sx hd-priv 0 | sx hd-priv 12 --hard | sx hd-priv 4 # generate m/0/12'/4 xprv9yL8ndfdPVeDWJenF18oiHguRUj8jHmVrqqD97YQHeTcR3LCeh53q5PXPkLsy2kRaqgwoS6YZBLatRZR\ yUeAkRPe1kLR1P6Mn7jUrXFquUt
Advanced Keys and Addresses
Encrypted Private Keys (BIP0038)
Private keys must remain secret. The need for confidentiality of the private keys is a truism which is quite difficult to achieve in practice, as it conflicts with the equally important security objective of availability. Keeping the private key private is much harder when you need to store backups of the private key to avoid losing it. A private key stored in a wallet that is encrypted by a password may be secure, but that wallet needs to be backed up. At times, users need to move keys from one wallet to another — to upgrade or replace the wallet software, for example. Private key backups might also be stored on paper (see “Paper Wallets” on page 105) or on external storage media, such as a USB flash drive. But what if the backup itself is stolen or lost? These conflicting security goals led to the introduction of a portable and convenient standard for en‐ crypting private keys in a way that can be understood by many different wallets and bitcoin clients, standardized by Bitcoin Improvement Proposal 38 or BIP0038
BIP0038 proposes a common standard for encrypting private keys with a passphrase and encoding them with Base58Check so that they can be stored securely on backup media, transported securely between wallets or in any other conditions where the key might be exposed. The standard for encryption uses the Advanced Encryption Standard (AES), a standard established by the National Institute of Standards and Technology (NIST) and used broadly in data encryption implementations for commercial and mili‐ tary applications.
A BIP0038 encryption scheme takes as input a bitcoin private key, usually encoded in the Wallet Import Format (WIF), as a Base58Check string with a prefix of “5”. Addi‐ tionally, the BIP0038 encryption scheme takes a passphrase — a long password — usu‐ ally composed of several words or a complex string of alphanumeric characters. The result of the BIP0038 encryption scheme is a Base58Check encoded encrypted private key that begins with the prefix 6P. If you see a key that starts with 6P that means it is encrypted and requires a passphrase in order to convert (decrypt) it back into a WIFformatted private key (prefix 5) that can be used in any wallet. Many wallet applications now recognize BIP0038 encrypted private keys and will prompt the user for a passphrase to decrypt and import the key. Third party applications, such as the incredibly useful browser-based bitaddress.org (Wallet Details tab), can be used to decrypt BIP0038 keys.
The most common use case for BIP0038 encrypted keys is for paper wallets that can be used to backup private keys on a piece of paper. As long as the user selects a strong passphrase, a paper wallet with BIP0038 encrypted private keys is incredibly secure and a great way to create offline bitcoin storage (also known as “cold storage”)
Test the following encrypted keys using bitaddress.org to see how you can get the de‐ crypted key by entering the passphrase:
Table 4-10. Example of BIP0038 Encrypted Private Key
Private Key (WIF) 5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2JpbnkeyhfsYB1Jcn Passphrase MyTestPassphrase Encrypted Key (BIP0038 6PRTHL6mWa48xSopbU1cKrVjpKbBZxcLRRCdctLJ3z5yxE87MobKoXdTsJ
Pay To Script Hash (P2SH) and Multi-Sig Addresses
As we know, traditional bitcoin addresses begin with the number “1” and are derived from the public key, which is derived from the private key. While anyone can send bitcoin to a “1” address, that bitcoin can only be spent by presenting the corresponding private key signature and public key hash.
Bitcoin addresses that begin with the number “3” are pay-to-script-hash (P2SH) ad‐ dresses, sometimes erroneously called multi-signature or multi-sig addresses. They designate the beneficiary of a bitcoin transaction as the hash of a script, instead of the owner of a public key. The feature was introduced in January 2012 with Bitcoin Im‐ provement Proposal 16 or BIP0016 and is being widely adopted because it provides the opportunity to add functionality to the address itself. Unlike transactions that “send” funds to traditional “1” bitcoin addresses, also known as pay-to-public-keyhash (P2PKH), funds sent to “3” addresses require something more than the presenta‐ tion of one public key hash and one private key signature as proof of ownership. The requirements are designated at the time the address is created, within the script, and all inputs to this address will be encumbered with the same requirements.
A pay-to-script-hash address is created from a transaction script, which defines who can spend a transaction output. Encoding a pay-to-script hash address involves using the same double-hash function as used during creation of a bitcoin address, only applied on the script instead of the public key.
script hash = RIPEMD160(SHA256(script))
The resulting “script hash” is encoded with Base58Check with a version prefix of 5, which results in an encoded address starting with a 3. An example of a P2SH address is 32M8ednmuyZ2zVbes4puqe44NZumgG92sM
P2SH is not necessarily the same as a multi-signature standard trans‐ action. A P2SH address most often represents a multi-signature script, but it might also represent a script encoding other types of transac‐ tions.
Multi-signature addresses and P2SH
Currently, the most common implementation of the P2SH function is the multisignature address script. As the name implies, the underlying script requires more than one signature to prove ownership and therefore spend funds. The bitcoin multisignature feature is designed to require M signatures (also known as the “threshold”) from a total of N keys, known as an M-of-N multi-sig, where M is equal to or less than N. For example, Bob the coffee shop owner from Chapter 1 could use a multi-signature address requiring 1-of-2 signatures from a key belonging to him and a key belonging to his spouse, ensuring either of them could sign to spend a transaction output locked to this address. This would be similar to a “joint account” as implemented in traditional banking where either spouse can spend with a single signature. Or Gopesh, the web designer paid by Bob to create a website might have a 2-of-3 multi-signature address for his business that ensures that no funds can be spent unless at least two of the business partners sign a transaction.
Vanity Addresses
Vanity addresses are valid bitcoin addresses that contain human-readable messages, for example 1LoveBPzzD72PUXLzCkYAtGFYmK5vYNR33 is a valid address that contains the letters forming the word “Love” as the first four Base-58 letters. Vanity addresses require generating and testing billions of candidate private keys, until one derives a bitcoin address with the desired pattern. While there are some optimizations in the vanity generation algorithm, the process essentially involves picking a private key at random, deriving the public key, deriving the bitcoin address and checking to see if it matches the desired vanity pattern, repeating billions of times until a match is found.
Once a vanity address matching the desired pattern is found, the private key from which it was derived can be used by the owner to spend bitcoins in exactly the same way as any other address. Vanity addresses are no less or more secure than any other address. They depend on the same Elliptic Curve Cryptography (ECC) and Secure Hash Algo‐ rithm (SHA) as any other address. You can no easier find the private key of an address starting with a vanity pattern than you can any other address.
In our first chapter, we introduced Eugenia, a children’s charity director operating in the Philippines. Let’s say that Eugenia is organizing a bitcoin fundraising drive and wants to use a vanity bitcoin address to publicize the fundraising. Eugenia will create a vanity address that starts with “1Kids”, to promote the children’s charity fundraiser. Let’s see how this vanity address will be created and what it means for the security of Eugenia’s charity.
Generating Vanity Addresses
It’s important to realize that a bitcoin address is simply a number represented by symbols in the Base-58 alphabet. The search for a pattern like “1Kids” can be seen as searching for an address in the range from “1Kids11111111111111111111111111111” to “1Kidszzzzzzzzzzzzzzzzzzzzzzzzzzzzz”. There are approximately 5829 (approximately 1.4 * 1051) addresses in that range, all starting with “1Kids”.
Table 4-11. The range of vanity addresses starting with “1Kids”
From 1Kids11111111111111111111111111111 To 1Kidszzzzzzzzzzzzzzzzzzzzzzzzzzzzz
Let’s look at the pattern “1Kids” as a number and see how frequently we might find this pattern in a bitcoin address. An average desktop computer PC, without any specialized hardware, can search approximately 100,000 keys per second.
Table 4-12. The frequency of a vanity pattern (1KidsCharity) and average time-to-find on a desktop PC
| Length | Pattern | Frequency | Average Search Time |
| 1 2 3 4 5 6 7 8 9 10 11 |
1K 1Ki 1Kid 1Kids 1KidsC 1KidsCh 1KidsCha 1KidsChar 1KidsChar 1KidsCharit 1KidsCharit |
1 in 58 keys 1 in 3,364 1 in 195,000 1 in 11 million 1 in 656 million 1 in 38 billion 1 in 2.2 trillion 1 in 128 trillion 1 in 7 quadrillion 1 in 7 quadrillion 1 in 23 quintillion 2 |
< 1 milliseconds 50 milliseconds < 2 seconds 1 minute 1 hour 2 days 3-4 months 13-18 years 800 years 46,000 years 2.5 million years |
As you can see, Eugenia won’t be creating the vanity address “1KidsCharity” any time soon, even if she had access to several thousand computers. Each additional character increases the difficulty by a factor of 58. Patterns with more than seven characters are usually found by specialized hardware, such as custom-built desktops with multiple Graphical Processing Units (GPUs). These are often re-purposed bitcoin mining “rigs” that are no longer profitable for bitcoin mining but can be used effectively to find vanity addresses. Vanity searches on GPU systems are many orders of magnitude faster than on a general-purpose CPU.
Another way to find a vanity address is to outsource the work to a pool of vanity-miners, such as the pool at vanitypool.appspot.com. A pool is a service that allows those with GPU hardware to earn bitcoin searching for vanity addresses for others. For a small payment (0.01 bitcoin or approximately $5 when this was written), Eugenia can out‐ source the search for a 7-character pattern vanity address and get results in a few hours instead of having to run a CPU search for months.
Generating a vanity address is a brute-force exercise: try a random key, check the re‐ sulting address to see if it matches the desired pattern, repeat until successful. Here’s an example of a “vanity miner”, a program designed to find vanity addresses, written in C ++.
Example- Vanity Address Miner
#include <bitcoin/bitcoin.hpp>
// The string we are searching for
const std::string search = "1kid";
// Generate a random secret key. A random 32 bytes.
bc::ec_secret random_secret(std::default_random_engine& engine);
// Extract the Bitcoin address from an EC secret.
std::string bitcoin_address(const bc::ec_secret& secret);
// Case insensitive comparison with the search string.
bool match_found(const std::string& address);
int main()
{
std::random_device random;
std::default_random_engine engine(random());
// Loop continuously...
while (true)
{
// Generate a random secret.
bc::ec_secret secret = random_secret(engine);
// Get the address.
std::string address = bitcoin_address(secret);
// Does it match our search string? (1kid)
if (match_found(address))
{
// Success!
std::cout << "Found vanity address! " << address << std::endl;
std::cout << "Secret: " << bc::encode_hex(secret) << std::endl;
return 0;
}
}
// Should never reach here!
return 0;
}
bc::ec_secret random_secret(std::default_random_engine& engine)
{
// Create new secret...
bc::ec_secret secret;
// Iterate through every byte setting a random value...
for (uint8_t& byte: secret)
byte = engine() % std::numeric_limits<uint8_t>::max();
// Return result.
return secret;
}
std::string bitcoin_address(const bc::ec_secret& secret)
{
// Convert secret to pubkey...
bc::ec_point pubkey = bc::secret_to_public_key(secret);
// Finally create address.
bc::payment_address payaddr;
bc::set_public_key(payaddr, pubkey);
// Return encoded form.
return payaddr.encoded();
}
bool match_found(const std::string& address)
{
auto addr_it = address.begin();
// Loop through the search string comparing it to the lower case
// character of the supplied address.
for (auto it = search.begin(); it != search.end(); ++it, ++addr_it)
if (*it != std::tolower(*addr_it))
return false;
// Reached end of search string, so address matches.
return true;
}
The example code must be compiled using a C++ compiler and linked against the lib‐ bitcoin library (which must be first installed on that system). To run the example, run the vanity-minder executable with no parameters and it will attempt to find a vanity address starting with “1kid”:
Example Compiling and running the vanity-miner example
$ # Compile the code with g++
$ g++ -o vanity-miner vanity-miner.cpp $(pkg-config --cflags --libs libbitcoin)
$ # Run the example
$ ./vanity-miner
Found vanity address! 1KiDzkG4MxmovZryZRj8tK81oQRhbZ46YT
Secret: 57cc268a05f83a23ac9d930bc8565bac4e277055f4794cbd1a39e5e71c038f3f
$ # Run it again for a different result
$ ./vanity-miner
Found vanity address! 1Kidxr3wsmMzzouwXibKfwTYs5Pau8TUFn
Secret: 7f65bbbbe6d8caae74a0c6a0d2d7b5c6663d71b60337299a1a2cf34c04b2a623
# Use "time" to see how long it takes to find a result
$ time ./vanity-miner
Found vanity address! 1KidPWhKgGRQWD5PP5TAnGfDyfWp5yceXM
Secret: 2a802e7a53d8aa237cd059377b616d2bfcfa4b0140bc85fa008f2d3d4b225349
real 0m8.868s
user 0m8.828s
sys 0m0.035sThe example code will take a few seconds to find a match for the three-character pattern “kid”, as we can see when we use the time Unix command to measure the execution time. Change the search pattern in the source code and see how much longer it takes for four- or five-character patterns!
Vanity Address Security
Vanity addresses can be used to enhance and to defeat security measures, they are truly a double-edged sword. Used to improve security, a distinctive address makes it harder for adversaries to substitute their own address and fool your customers into paying them instead of you. Unfortunately, vanity addresses also make it possible for anyone to create an address that resembles any random address, or even another vanity address, thereby fooling your customers.
Eugenia could advertise a randomly generated address (e.g. 1J7mdg5rbQyUHE‐ NYdx39WVWK7fsLpEoXZy) to which people can send their donations. Or, she could generate a vanity address that starts with 1Kids, to make it more distinctive.
In both cases, one of the risks of using a single fixed address (rather than a separate dynamic address per donor) is that a thief might be able to infiltrate your website and replace it with their own address, thereby diverting donations to themselves. If you have advertised your donation address in a number of different places, your users may vis‐ ually inspect the address before making a payment to ensure it is the same one they saw on your website, on your email, and on your flyer. In the case of a random address like “1J7mdg5rbQyUHENYdx39WVWK7fsLpEoXZy”, the average user will inspect the first few characters “1J7mdg” perhaps and be satisfied that the address matches. Using a vanity address generator, someone with the intent to steal by substituting a similarlooking address can quickly generate addresses that match the first few characters:
Table Generating vanity addresses to match a random address
Original Random Address 1 1J7mdg5rbQyUHENYdx39WVWK7fsLpEoXZy Vanity (4 character match) 1J7md1QqU4LpctBetHS2ZoyLV5d6dShhEy Vanity (5 character match) 1J7mdgYqyNd4ya3UEcq31Q7sqRMXw2XZ6n Vanity (6 character match) 1J7mdg5WxGENmwyJP9xuGhG5KRzu99BBCX
So does a vanity address increase security? If Eugenia generates the vanity address “1Kids33q44erFfpeXrmDSz7zEqG2FesZEN”, users are likely to look at the vanity pat‐ tern word and a few characters beyond, for example noticing the “1Kids33” part of the address. That would force an attacker to generate a vanity address matching at least 6 characters (2 more), expending an effort that is 3,364 times (58 x 58) higher than the effort Eugenia expended for her 4 character vanity. Essentially, the effort Eugenia ex‐ pends (or pays a vanity pool for) “pushes” the attacker into having to produce a longer pattern vanity. If Eugenia pays a pool to generate an 8 character vanity address, the attacker would be pushed into the realm of 10 characters which is infeasible on a per‐ sonal computer and expensive even with a custom vanity-mining rig or vanity pool. What is affordable for Eugenia becomes unaffordable for the attacker, especially if the potential reward of fraud is not high enough to cover the cost of the vanity address generation.
Paper Wallets
Paper wallets are bitcoin private keys printed on paper. Often the paper wallet also includes the corresponding bitcoin address, for convenience, but this is not necessary since it can be derived from the private key. Paper wallets are a very effective way to create backups or offline bitcoin storage, also known as “cold storage”. As a backup mechanism, a paper wallet can provide security against the loss of key due to a computer mishap such as a hard drive failure, theft, or accidental deletion. As a “cold storage” mechanism, if the paper wallet keys are generated offline and never stored on a computer system, they are much more secure against hackers, key-loggers and other online com‐ puter threats.
Paper wallets come in many shapes, sizes and designs, but at a very basic level are just a key and an address printed on paper. Here’s the simplest form of a paper wallet:
Table A very simple paper wallet – a printout of the bitcoin address and private key
Public Address 1424C2F4bC9JidNjjTUZCbUxv6Sa1Mt62x Private Key (WIF) 5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2JpbnkeyhfsYB1Jcn
Paper wallets can be generated easily using a tool such as the client-side Javascript gen‐ erator at bitaddress.org. This page contains all the code necessary to generate keys and paper wallets, even while completely disconnected from the Internet. To use it, save the HTML page on your local drive or on an external USB flash drive. Disconnect from the Internet and open the file in a browser. Even better, boot your computer using a pristine operating system, such as a CDROM bootable Linux OS. Any keys generated with this tool while offline can be printed on a local printer over a USB cable (not wirelessly), thereby creating paper wallets whose keys exist only on the paper and have never been stored on any online system. Put these paper wallets in a fire-proof safe and “send” bitcoin to their bitcoin address, to implement a simple yet highly effective “cold storage” solution.

The disadvantage of the simple paper wallet system is that the printed keys are vulnerable to theft. A thief who is able to gain access to the paper can either steal it or photograph the keys and take control of the bitcoins locked with those keys. A more sophisticated paper wallet storage system uses BIP0038 encrypted private keys. The keys printed on the paper wallet are protected by a passphrase that the owner has memorized. Without the passphrase, the encrypted keys are useless. Yet, they still are superior to a passphrase protected wallet because the keys have never been online and must be physically re‐ trieved from a safe or other physically secured storage.

While you can deposit funds into a paper wallet several times, you should withdraw all funds only once, spending everything. This is because in the process of unlocking and spending funds you ex‐ pose the private key and because some wallets may generate a change address if you spend less than the whole amount. One way to do this is to withdraw the entire balance stored in the paper wallet and send any remaining funds to a new paper wallet.
Paper wallets come in many designs and sizes, with many different features. Some are intended to be given as gifts and have seasonal themes, such as Christmas and New Year’s themes. Others are designed for storage in a bank vault or safe with the private key hidden in some way, either with opaque scratch-off stickers, or folded and sealed with tamper-proof adhesive foil.

Other designs feature additional copies of the key and address, in the form of detachable stubs similar to ticket stubs, allowing you to store multiple copies to protect against fire, flood or other natural disasters.

This article has been published from the source link without modifications to the text. Only the headline has been changed.