Mathematical functions are important to know as a data scientist, because we want to make predictions and interpret them.
Linear Functions
In mathematics a function is used to relate one variable to another variable.
Suppose we consider the relationship between calorie burnage and average pulse. It is reasonable to assume that, in general, the calorie burnage will change as the average pulse changes – we say that the calorie burnage depends upon the average pulse.
Furthermore, it may be reasonable to assume that as the average pulse increases, so will the calorie burnage. Calorie burnage and average pulse are the two variables being considered.
Because the calorie burnage depends upon the average pulse, we say that calorie burnage is the dependent variable and the average pulse is the independent variable.
The relationship between a dependent and an independent variable can often be expressed mathematically using a formula (function).
A linear function has one independent variable (x) and one dependent variable (y), and has the following form:
y = f(x) = ax + b
This function is used to calculate a value for the dependent variable when we choose a value for the independent variable.
Explanation:
- f(x) = the output (the dependant variable)
- x = the input (the independant variable)
- a = slope = is the coefficient of the independent variable. It gives the rate of change of the dependent variable
- b = intercept = is the value of the dependent variable when x = 0. It is also the point where the diagonal line crosses the vertical axis.
Linear Function With One Explanatory Variable
A function with one explanatory variable means that we use one variable for prediction.
Let us say we want to predict calorie burnage using average pulse. We have the following formula:
f(x) = 2x + 80
Here, the numbers and variables means:
- f(x) = The output. This number is where we get the predicted value of Calorie_Burnage
- x = The input, which is Average_Pulse
- 2 = Slope = Specifies how much Calorie_Burnage increases if Average_Pulse increases by one. It tells us how “steep” the diagonal line is
- 80 = Intercept = A fixed value. It is the value of the dependent variable when x = 0
Plotting a Linear Function
The term linearity means a “straight line”. So, if you show a linear function graphically, the line will always be a straight line. The line can slope upwards, downwards, and in some cases may be horizontal or vertical.
Here is a graphical representation of the mathematical function above:
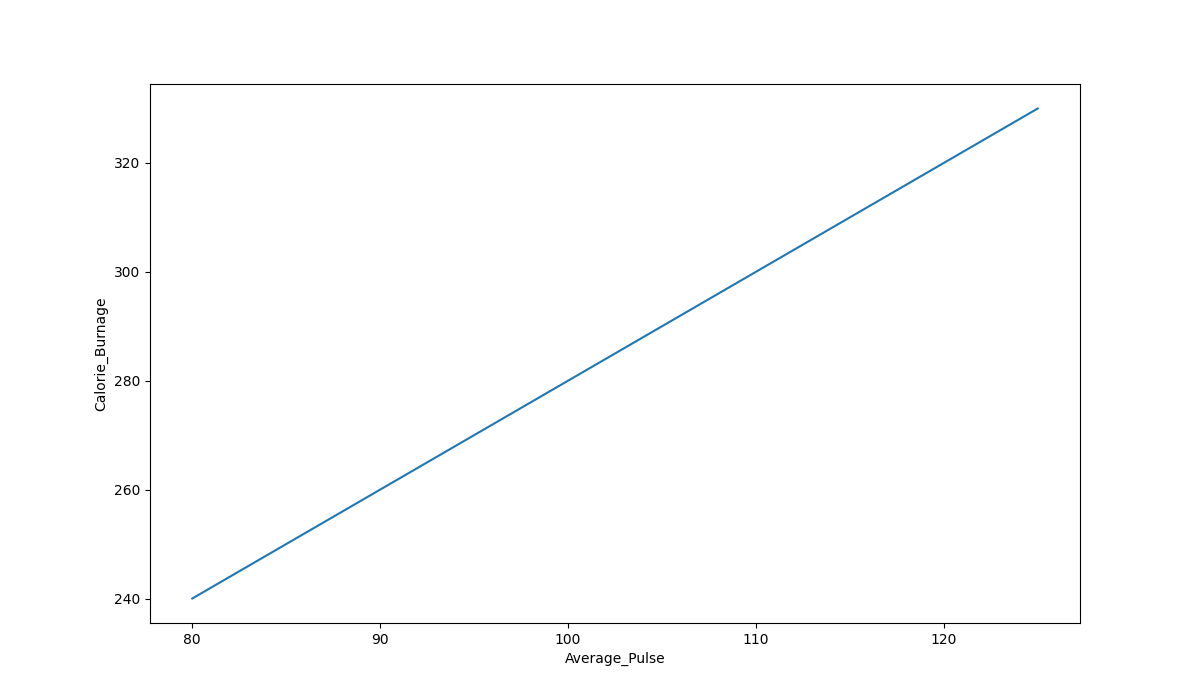
Graph Explanations:
- The horizontal axis is generally called the x-axis. Here, it represents Average_Pulse.
- The vertical axis is generally called the y-axis. Here, it represents Calorie_Burnage.
- Calorie_Burnage is a function of Average_Pulse, because Calorie_Burnage is assumed to be dependent on Average_Pulse.
- In other words, we use Average_Pulse to predict Calorie_Burnage.
- The blue (diagonal) line represents the structure of the mathematical function that predicts calorie burnage.
Data Science – Plotting Linear Functions
The Sports Watch Data Set
Take a look at our health data set:
| Duration | Average_Pulse | Max_Pulse | Calorie_Burnage | Hours_Work | Hours_Sleep |
|---|---|---|---|---|---|
| 30 | 80 | 120 | 240 | 10 | 7 |
| 30 | 85 | 120 | 250 | 10 | 7 |
| 45 | 90 | 130 | 260 | 8 | 7 |
| 45 | 95 | 130 | 270 | 8 | 7 |
| 45 | 100 | 140 | 280 | 0 | 7 |
| 60 | 105 | 140 | 290 | 7 | 8 |
| 60 | 110 | 145 | 300 | 7 | 8 |
| 60 | 115 | 145 | 310 | 8 | 8 |
| 75 | 120 | 150 | 320 | 0 | 8 |
| 75 | 125 | 150 | 330 | 8 | 8 |
Plot the Existing Data in Python
Now, we can first plot the values of Average_Pulse against Calorie_Burnage using the matplotlib library.
The plot() function is used to make a 2D hexagonal binning plot of points x,y:
Example
import matplotlib.pyplot as plt
health_data.plot(x =‘Average_Pulse’, y=‘Calorie_Burnage’, kind=‘line’),
plt.ylim(ymin=0)
plt.xlim(xmin=0)
plt.show()
Example Explained
- Import the pyplot module of the matplotlib library
- Plot the data from Average_Pulse against Calorie_Burnage
kind='line'tells us which type of plot we want. Here, we want to have a straight line- plt.ylim() and plt.xlim() tells us what value we want the axis to start on. Here, we want the axis to begin from zero
- plt.show() shows us the output
The code above will produce the following result:
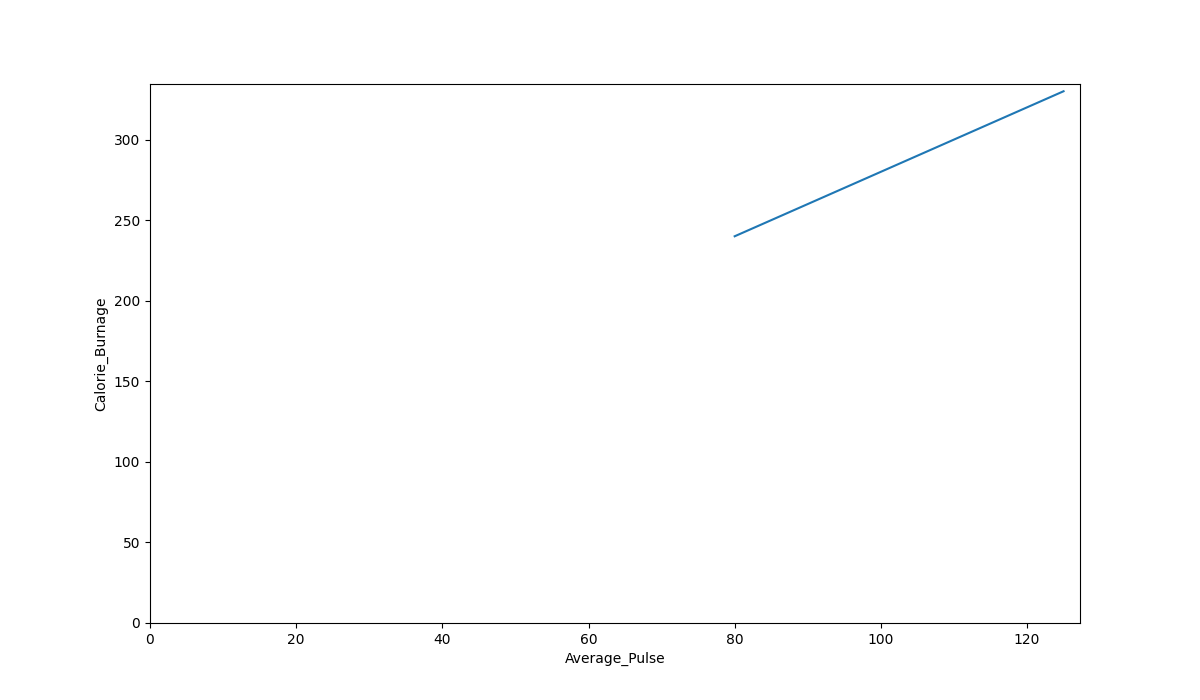
The Graph Output
As we can see, there is a relationship between Average_Pulse and Calorie_Burnage. Calorie_Burnage increases proportionally with Average_Pulse. It means that we can use Average_Pulse to predict Calorie_Burnage.
Why is The Line Not Fully Drawn Down to The y-axis?
The reason is that we do not have observations where Average_Pulse or Calorie_Burnage are equal to zero. 80 is the first observation of Average_Pulse and 240 is the first observation of Calorie_Burnage
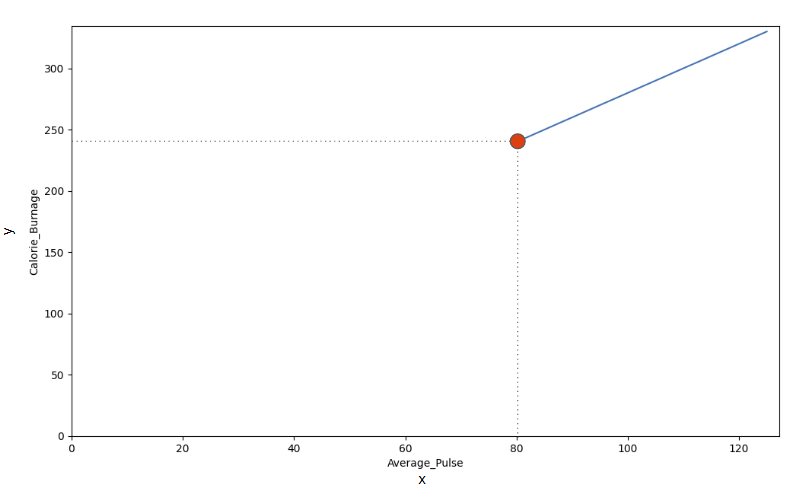
Look at the line. What happens to calorie burnage if average pulse increases from 80 to 90?
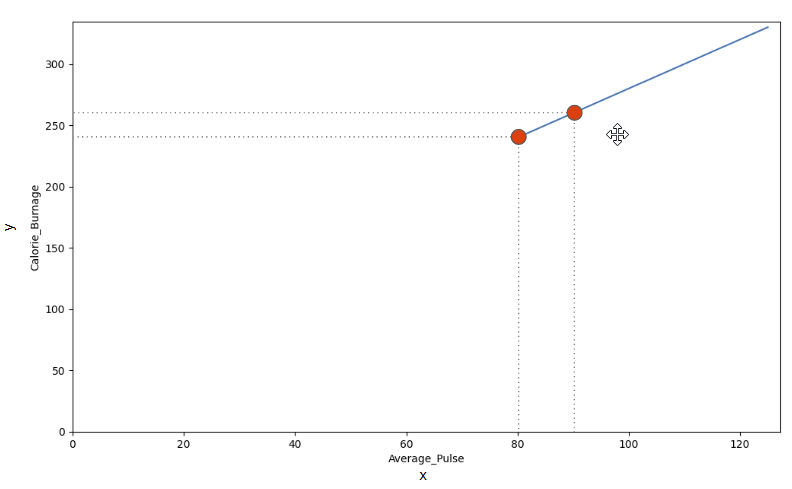
We can use the diagonal line to find the mathematical function to predict calorie burnage.
As it turns out:
- If the average pulse is 80, the calorie burnage is 240
- If the average pulse is 90, the calorie burnage is 260
- If the average pulse is 100, the calorie burnage is 280
There is a pattern. If average pulse increases by 10, the calorie burnage increases by 20.
Slope and Intercept
This section will explain how we find the slope and intercept in data science:
f(x) = 2x + 80
The image below points to the Slope – which indicates how steep the line is, and the Intercept – which is the value of y, when x = 0 (the point where the diagonal line crosses the vertical axis). The red line is the continuation of the blue line from previous page.
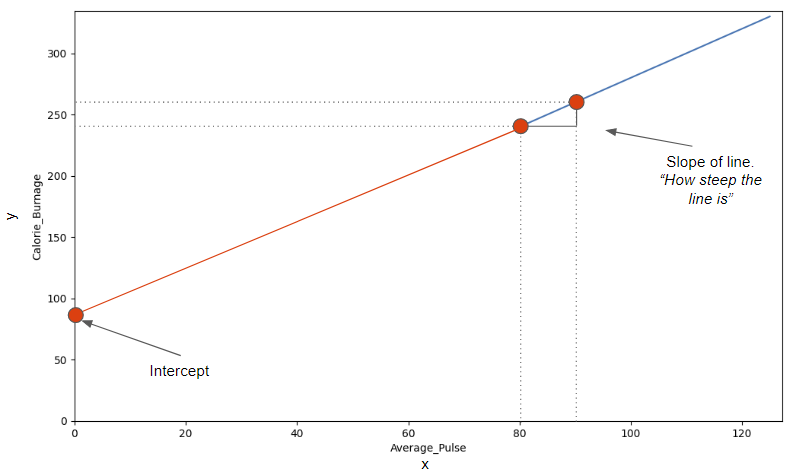

Find The Slope
The slope is defined as how much calorie burnage increases, if average pulse increases by one. It tells us how “steep” the diagonal line is.
We can find the slope by using the proportional difference of two points from the graph.
- If the average pulse is 80, the calorie burnage is 240
- If the average pulse is 90, the calorie burnage is 260
We see that if average pulse increases with 10, the calorie burnage increases by 20.
Slope = 20/10 = 2
The slope is 2.
Mathematically, Slope is Defined as:
Slope = f(x2) - f(x1) / x2-x1
f(x2) = Second observation of Calorie_Burnage = 260
f(x1) = First observation of Calorie_Burnage = 240
x2 = Second observation of Average_Pulse = 90
x1 = First observation of Average_Pulse = 80
Slope = (260-240) / (90 – 80) = 2
Be consistent to define the observations in the correct order! If not, the prediction will not be correct!
Use Python to Find the Slope
Calculate the slope with the following code:
Example
def slope(x1, y1, x2, y2):
s = (y2-y1)/(x2-x1)
return s
print (slope(80,240,90,260))
Find The Intercept
The intercept is used to fine tune the functions ability to predict Calorie_Burnage.
The intercept is where the diagonal line crosses the y-axis, if it were fully drawn.
The intercept is the value of y, when x = 0.
Here, we see that if average pulse (x) is zero, then the calorie burnage (y) is 80.
So, the intercept is 80.
Sometimes, the intercept has a practical meaning. Sometimes not.
Does it make sense that average pulse is zero?
No, you would be dead and you certainly would not burn any calories.
However, we need to include the intercept in order to complete the mathematical function’s ability to predict Calorie_Burnage correctly.
Other examples where the intercept of a mathematical function can have a practical meaning:
- Predicting next years revenue by using marketing expenditure (How much revenue will we have next year, if marketing expenditure is zero?). It is likely to assume that a company will still have some revenue even though if it does not spend money on marketing.
- Fuel usage with speed (How much fuel do we use if speed is equal to 0 mph?). A car that uses gasoline will still use fuel when it is idle.
Find the Slope and Intercept Using Python
The np.polyfit() function returns the slope and intercept.
If we proceed with the following code, we can both get the slope and intercept from the function.
Example
import numpy as np
health_data = pd.read_csv("data.csv", header=0, sep=",")
x = health_data["Average_Pulse"]
y = health_data["Calorie_Burnage"]
slope_intercept = np.polyfit(x,y,1)
print(slope_intercept)
Example Explained:
- Isolate the variables Average_Pulse (x) and Calorie_Burnage (y) from health_data.
- Call the np.polyfit() function.
- The last parameter of the function specifies the degree of the function, which in this case is “1”.
Tip: linear functions = 1.degree function. In our example, the function is linear, which is in the 1.degree. That means that all coefficients (the numbers) are in the power of one.
We have now calculated the slope (2) and the intercept (80). We can write the mathematical function as follow:
Predict Calorie_Burnage by using a mathematical expression:
f(x) = 2x + 80
Task:
Now, we want to predict calorie burnage if average pulse is 135.
Remember that the intercept is a constant. A constant is a number that does not change.
We can now substitute the input x with 135:
f(135) = 2 * 135 + 80 = 350
If average pulse is 135, the calorie burnage is 350.
Define the Mathematical Function in Python
Here is the exact same mathematical function, but in Python. The function returns 2*x + 80, with x as the input:
Example
def my_function(x):
return 2*x + 80
print (my_function(135))
Try to replace x with 140 and 150.
Plot a New Graph in Python
Here, we plot the same graph as earlier, but formatted the axis a little bit.
Max value of the y-axis is now 400 and for x-axis is 150:
Example
import matplotlib.pyplot as plt
health_data.plot(x ='Average_Pulse', y='Calorie_Burnage', kind='line'),
plt.ylim(ymin=0, ymax=400)
plt.xlim(xmin=0, xmax=150)
plt.show()
Example Explained
- Import the pyplot module of the matplotlib library
- Plot the data from Average_Pulse against Calorie_Burnage
kind='line'tells us which type of plot we want. Here, we want to have a straight line- plt.ylim() and plt.xlim() tells us what value we want the axis to start and stop on.
- plt.show() shows us the output
This article has been published from the source link without modifications to the text. Only the headline has been changed.




