Support Vector Machine or SVM is one of the most popular Supervised Learning algorithms, which is used for Classification as well as Regression problems. However, primarily, it is used for Classification problems in Machine Learning.
The goal of the SVM algorithm is to create the best line or decision boundary that can segregate n-dimensional space into classes so that we can easily put the new data point in the correct category in the future. This best decision boundary is called a hyperplane.
SVM chooses the extreme points/vectors that help in creating the hyperplane. These extreme cases are called as support vectors, and hence algorithm is termed as Support Vector Machine. Consider the below diagram in which there are two different categories that are classified using a decision boundary or hyperplane:
Example: SVM can be understood with the example that we have used in the KNN classifier. Suppose we see a strange cat that also has some features of dogs, so if we want a model that can accurately identify whether it is a cat or dog, so such a model can be created by using the SVM algorithm. We will first train our model with lots of images of cats and dogs so that it can learn about different features of cats and dogs, and then we test it with this strange creature. So as support vector creates a decision boundary between these two data (cat and dog) and choose extreme cases (support vectors), it will see the extreme case of cat and dog. On the basis of the support vectors, it will classify it as a cat. Consider the below diagram:
SVM algorithm can be used for Face detection, image classification, text categorization, etc.
Types of SVM
SVM can be of two types:
- Linear SVM: Linear SVM is used for linearly separable data, which means if a dataset can be classified into two classes by using a single straight line, then such data is termed as linearly separable data, and classifier is used called as Linear SVM classifier.
- Non-linear SVM: Non-Linear SVM is used for non-linearly separated data, which means if a dataset cannot be classified by using a straight line, then such data is termed as non-linear data and classifier used is called as Non-linear SVM classifier.
Hyperplane and Support Vectors in the SVM algorithm:
Hyperplane: There can be multiple lines/decision boundaries to segregate the classes in n-dimensional space, but we need to find out the best decision boundary that helps to classify the data points. This best boundary is known as the hyperplane of SVM.
The dimensions of the hyperplane depend on the features present in the dataset, which means if there are 2 features (as shown in image), then hyperplane will be a straight line. And if there are 3 features, then hyperplane will be a 2-dimension plane.
We always create a hyperplane that has a maximum margin, which means the maximum distance between the data points.
Support Vectors:
The data points or vectors that are the closest to the hyperplane and which affect the position of the hyperplane are termed as Support Vector. Since these vectors support the hyperplane, hence called a Support vector.
How does SVM works?
Linear SVM:
The working of the SVM algorithm can be understood by using an example. Suppose we have a dataset that has two tags (green and blue), and the dataset has two features x1 and x2. We want a classifier that can classify the pair(x1, x2) of coordinates in either green or blue. Consider the below image:
So as it is 2-d space so by just using a straight line, we can easily separate these two classes. But there can be multiple lines that can separate these classes. Consider the below image:
Hence, the SVM algorithm helps to find the best line or decision boundary; this best boundary or region is called as a hyperplane. SVM algorithm finds the closest point of the lines from both the classes. These points are called support vectors. The distance between the vectors and the hyperplane is called as margin. And the goal of SVM is to maximize this margin. The hyperplane with maximum margin is called the optimal hyperplane.
Non-Linear SVM:
If data is linearly arranged, then we can separate it by using a straight line, but for non-linear data, we cannot draw a single straight line. Consider the below image:
So to separate these data points, we need to add one more dimension. For linear data, we have used two dimensions x and y, so for non-linear data, we will add a third dimension z. It can be calculated as:
z=x2 +y2
By adding the third dimension, the sample space will become as below image:
So now, SVM will divide the datasets into classes in the following way. Consider the below image:
Since we are in 3-d Space, hence it is looking like a plane parallel to the x-axis. If we convert it in 2d space with z=1, then it will become as:
Hence we get a circumference of radius 1 in case of non-linear data.
Python Implementation of Support Vector Machine
Now we will implement the SVM algorithm using Python. Here we will use the same dataset user_data, which we have used in Logistic regression and KNN classification.
- Data Pre-processing step
Till the Data pre-processing step, the code will remain the same. Below is the code:
- #Data Pre-processing Step
- # importing libraries
- import numpy as nm
- import matplotlib.pyplot as mtp
- import pandas as pd
- #importing datasets
- data_set= pd.read_csv(‘user_data.csv’)
- #Extracting Independent and dependent Variable
- x= data_set.iloc[:, [2,3]].values
- y= data_set.iloc[:, 4].values
- # Splitting the dataset into training and test set.
- from sklearn.model_selection import train_test_split
- x_train, x_test, y_train, y_test= train_test_split(x, y, test_size= 0.25, random_state=0)
- #feature Scaling
- from sklearn.preprocessing import StandardScaler
- st_x= StandardScaler()
- x_train= st_x.fit_transform(x_train)
- x_test= st_x.transform(x_test)
After executing the above code, we will pre-process the data. The code will give the dataset as:
The scaled output for the test set will be:
Fitting the SVM classifier to the training set:
Now the training set will be fitted to the SVM classifier. To create the SVM classifier, we will import SVC class from Sklearn.svm library. Below is the code for it:
- from sklearn.svm import SVC # “Support vector classifier”
- classifier = SVC(kernel=‘linear’, random_state=0)
- classifier.fit(x_train, y_train)
In the above code, we have used kernel=’linear’, as here we are creating SVM for linearly separable data. However, we can change it for non-linear data. And then we fitted the classifier to the training dataset(x_train, y_train)
Output:
Out[8]:
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovr', degree=3, gamma='auto_deprecated',
kernel='linear', max_iter=-1, probability=False, random_state=0,
shrinking=True, tol=0.001, verbose=False)
The model performance can be altered by changing the value of C(Regularization factor), gamma, and kernel.
- Predicting the test set result:
Now, we will predict the output for test set. For this, we will create a new vector y_pred. Below is the code for it:
- #Predicting the test set result
- y_pred= classifier.predict(x_test)
After getting the y_pred vector, we can compare the result of y_pred and y_test to check the difference between the actual value and predicted value.
Output: Below is the output for the prediction of the test set:
- Creating the confusion matrix:
Now we will see the performance of the SVM classifier that how many incorrect predictions are there as compared to the Logistic regression classifier. To create the confusion matrix, we need to import the confusion_matrix function of the sklearn library. After importing the function, we will call it using a new variable cm. The function takes two parameters, mainly y_true( the actual values) and y_pred (the targeted value return by the classifier). Below is the code for it:
- #Creating the Confusion matrix
- from sklearn.metrics import confusion_matrix
- cm= confusion_matrix(y_test, y_pred)
Output:
As we can see in the above output image, there are 66+24= 90 correct predictions and 8+2= 10 correct predictions. Therefore we can say that our SVM model improved as compared to the Logistic regression model.
- Visualizing the training set result:
Now we will visualize the training set result, below is the code for it:
- from matplotlib.colors import ListedColormap
- x_set, y_set = x_train, y_train
- x1, x2 = nm.meshgrid(nm.arange(start = x_set[:, 0].min() – 1, stop = x_set[:, 0].max() + 1, step =0.01),
- nm.arange(start = x_set[:, 1].min() – 1, stop = x_set[:, 1].max() + 1, step = 0.01))
- mtp.contourf(x1, x2, classifier.predict(nm.array([x1.ravel(), x2.ravel()]).T).reshape(x1.shape),
- alpha = 0.75, cmap = ListedColormap((‘red’, ‘green’)))
- mtp.xlim(x1.min(), x1.max())
- mtp.ylim(x2.min(), x2.max())
- for i, j in enumerate(nm.unique(y_set)):
- mtp.scatter(x_set[y_set == j, 0], x_set[y_set == j, 1],
- c = ListedColormap((‘red’, ‘green’))(i), label = j)
- mtp.title(‘SVM classifier (Training set)’)
- mtp.xlabel(‘Age’)
- mtp.ylabel(‘Estimated Salary’)
- mtp.legend()
- mtp.show()
Output:
By executing the above code, we will get the output as:
As we can see, the above output is appearing similar to the Logistic regression output. In the output, we got the straight line as hyperplane because we have used a linear kernel in the classifier. And we have also discussed above that for the 2d space, the hyperplane in SVM is a straight line.
- Visualizing the test set result:
- #Visulaizing the test set result
- from matplotlib.colors import ListedColormap
- x_set, y_set = x_test, y_test
- x1, x2 = nm.meshgrid(nm.arange(start = x_set[:, 0].min() – 1, stop = x_set[:, 0].max() + 1, step =0.01),
- nm.arange(start = x_set[:, 1].min() – 1, stop = x_set[:, 1].max() + 1, step = 0.01))
- mtp.contourf(x1, x2, classifier.predict(nm.array([x1.ravel(), x2.ravel()]).T).reshape(x1.shape),
- alpha = 0.75, cmap = ListedColormap((‘red’,‘green’ )))
- mtp.xlim(x1.min(), x1.max())
- mtp.ylim(x2.min(), x2.max())
- for i, j in enumerate(nm.unique(y_set)):
- mtp.scatter(x_set[y_set == j, 0], x_set[y_set == j, 1],
- c = ListedColormap((‘red’, ‘green’))(i), label = j)
- mtp.title(‘SVM classifier (Test set)’)
- mtp.xlabel(‘Age’)
- mtp.ylabel(‘Estimated Salary’)
- mtp.legend()
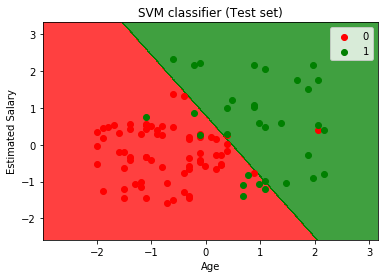
- mtp.show()
Output:
By executing the above code, we will get the output as:
As we can see in the above output image, the SVM classifier has divided the users into two regions (Purchased or Not purchased). Users who purchased the SUV are in the red region with the red scatter points. And users who did not purchase the SUV are in the green region with green scatter points. The hyperplane has divided the two classes into Purchased and not purchased variable.
This article has been published from the source link without modifications to the text. Only the headline has been changed.
Source link