The widespread success of deep learning across a range of domains such as natural language processing, conversational agents, and connectomics, has transformed the landscape of research in machine learning and left researchers with a number of interesting and important open questions such as: Why do deep neural networks (DNNs) generalize so well despite being overparameterized? What is the relationship between architecture, training, and performance for deep networks? How can one extract salient features from deep learning models?
One of the key theoretical insights that has allowed us to make progress in recent years has been that increasing the width of DNNs results in more regular behavior, and makes them easier to understand. A number of recent results have shown that DNNs that are allowed to become infinitely wide converge to another, simpler, class of models called Gaussian processes. In this limit, complicated phenomena (like Bayesian inference or gradient descent dynamics of a convolutional neural network) boil down to simple linear algebra equations. Insights from these infinitely wide networks frequently carry over to their finite counterparts. As such, infinite-width networks can be used as a lens to study deep learning, but also as useful models in their own right.
| Left: A schematic showing how deep neural networks induce simple input / output maps as they become infinitely wide. Right: As the width of a neural network increases , we see that the distribution of outputs over different random instantiations of the network becomes Gaussian. |
Unfortunately, deriving the infinite-width limit of a finite network requires significant mathematical expertise and has to be worked out separately for each architecture studied. Once the infinite-width model is derived, coming up with an efficient and scalable implementation further requires significant engineering proficiency. Together, the process of taking a finite-width model to its corresponding infinite-width network could take months and might be the topic of a research paper in its own right.
To address this issue and to accelerate theoretical progress in deep learning, we present Neural Tangents, a new open-source software library written in JAX that allows researchers to build and train infinitely wide neural networks as easily as finite neural networks. At its core, Neural Tangents provides an easy-to-use neural network library that builds finite- and infinite-width versions of neural networks simultaneously.
As an example of the utility of Neural Tangents, imagine training a fully-connected neural network on some data. Normally, a neural network is randomly initialized and then trained using gradient descent. Initializing and training many of these neural networks results in an ensemble. Often researchers and practitioners average the predictions from different members of the ensemble together for better performance. Additionally, the variance in the predictions of members of the ensemble can be used to estimate uncertainty. The downside is that training an ensemble of networks requires a significant computational budget, so it is often avoided. However, when the neural networks become infinitely wide, the ensemble is described by a Gaussian process with a mean and variance that can be computed throughout training.
With Neural Tangents, one can construct and train ensembles of these infinite-width networks at once using only five lines of code! The resulting training process is displayed below, and an interactive colaboratory notebook going through this experiment can be found here.
 |
| In both plots we compare training of an ensemble of finite neural networks with the infinite-width ensemble of the same architecture. The empirical mean and variance of the finite ensemble is displayed as a dashed black line between two dotted black lines. The closed-form mean and variance of the infinite-width ensemble is displayed as a solid colored line inside a filled color region. In both plots finite- and infinite-width ensembles match very closely and can be hard to distinguish. Left: Outputs (vertical f-axis) on the input data (horizontal x-axis) as the training progresses. Right: Train and test loss with uncertainty over the course of training. |
Despite the fact that the infinite-width ensemble is governed by a simple closed-form expression, it exhibits remarkable agreement with the finite-width ensemble. And since the infinite-width ensemble is a Gaussian process, it naturally provides closed-form uncertainty estimates (filled colored regions in the figure above). These uncertainty estimates closely match the variation of predictions that are observed when training many different copies of the finite network (dashed lines).
The above example shows the power of infinite-width neural networks to capture training dynamics. However, networks built using Neural Tangents can be applied to any problem on which you could apply a regular neural network. For example, below we compare three different infinite-width neural network architectures on image recognition using the CIFAR-10 dataset. Remarkably, we can evaluate ensembles of highly-elaborate models like infinitely wide residual networks in closed-form under both gradient descent and fully-Bayesian inference (an intractable task in the finite-width regime).
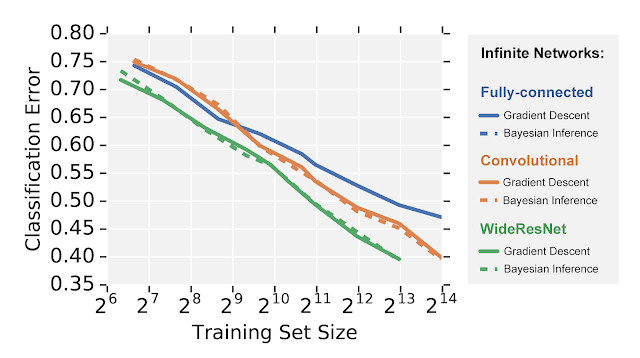
We see that, mimicking finite neural networks, infinite-width networks follow a similar hierarchy of performance with fully-connected networks performing worse than convolutional networks, which in turn perform worse than wide residual networks. However, unlike regular training, the learning dynamics of these models is completely tractable in closed-form, which allows unprecedented insight into their behavior.
We invite everyone to explore the infinite-width versions of their models with Neural Tangents, and help us open the black box of deep learning. To get started, please check out the paper, the tutorial Colab notebook, and the Github repo — contributions, feature requests, and bug reports are very welcome. This work has been accepted as a spotlight at ICLR 2020.
This article has been published from the source link without modifications to the text. Only the headline has been changed.
Source link




