Anomaly detectors are a key part of building robust distributed software. They enhance understanding of system behavior, speed up technical support, and improve root cause analysis. Find out more about their impact, and how new techniques from machine learning can further improve their performance.
What are anomaly detectors used for?
Modern software applications are often comprised of distributed microservices. Consider typical Software as a Service (SaaS) applications, which are accessed through web interfaces and run on the cloud. In part due to their physically distributed nature, managing and monitoring performance in these complex systems is becoming increasingly difficult. When issues such as performance degradations arise, it can be challenging to identify and debug the root causes. At Ericsson’s Global AI Accelerator, we’re exploring data-science based monitoring solutions that can learn to identify and categorize anomalous system behavior, and thereby improve incident resolution times.
Consider a customer logging onto their service provider’s website to add more data to their cell phone plan. Upon submitting their order, the website times out. When the user calls tech support, it may be unclear where in the application stack the error is occurring, and why. Is the error being triggered in the software’s frontend or backend? Is the network overloaded or is a database server locked up? The typical technical support process of manually searching through log files to diagnose the problem can be a long, labor-intensive process. By automating root cause analysis through the use of an anomaly detection framework, and building models for predictive maintenance, we can enhance the service provider’s situational understanding of the system and resolve incidents faster.
Setting realistic expectations
Before deploying an anomaly detection system, it’s important to set realistic expectations. In their book Anomaly Detection for Monitoring, Preetam Jinka and Baron Schwartz list what a perfect anomaly detector would do, common misconceptions surrounding their development, use, and performance, and what we can expect from a real-world anomaly detector.
The perfect anomaly-detection framework would:
- Automatically detect unusual changes in system behavior
- Predict major failures with 100% accuracy
- Provide easy-to-understand root cause analysis, so that service providers know exactly how to fix the issues at hand
In reality:
- No anomaly detector can provide 100% correct yes/no answers. False positives and false negatives will always exist, and there are trade-offs between the two
- No anomaly detector can provide 100% correct root cause analysis, possibly due to low signal-to-noise ratios, and correlation between performance indicators. Service providers must often infer causality by combining the results of anomaly detection with their domain or institutional knowledge
Additional challenges make this task difficult:
- The amount of data for training and testing the model may be limited, and it may not be labeled (i.e., we don’t know which data points are anomalies). Machine learning algorithms typically require large amounts of data, since anomalies are by definition statistically unlikely (i.e., anomalous behavior is less likely than normal behavior), datasets are often imbalanced (i.e., there are more occurrences of normal behavior than of anomalous behavior), which presents additional challenges in training models that accurately identify or predict anomalies
- Anomaly detectors may be built on dynamic systems with rapidly growing user bases. As a result, anomaly detectors have to adapt their behavior over time, as the underlying system evolves
Single-variable anomaly detection
A baseline univariate anomaly detector can be constructed by following these steps:
- First, calculate the arithmetic mean m and standard deviation s of the metric or indicator of interest over a sliding window. For example, calculate the mean and standard deviation of network latency over the previous two hours
- Second, calculate the corresponding z-score z=(v-m)/s (the z-score is a measure of how many standard deviations the measure is from the metric average)
- Third, classify points as anomalies if their z-score exceeds a pre-defined threshold. A z-score of three, corresponding to three standard deviations away from the mean (if we assume normally distributed data, approximately 3 out of 1000 data points are more than three standard deviations away from the mean), is a good starting point. In practice, the threshold value should be set following both statistical and domain considerations
Figure 1 – The anomaly detector estimates the anomaly bounds (blue) at each point in time using the mean and standard deviation of the target (black) over a 30-minute sliding window.
A problem with this approach, however, is that the anomaly bounds are strongly affected by outliers (Figure 1). Since the mean and standard deviation of the metric (or indicator of interest) are calculated over a sliding window, an anomaly occurring immediately after one of these outliers may be erroneously classified as a “normal” data point. The anomaly detector can be made more robust by instead calculating the z-score with the median and median-absolute-deviation, instead of the mean and standard deviation. This results in anomaly bounds that change more smoothly over time (Figure 2) and therefore anomalies are better classified.
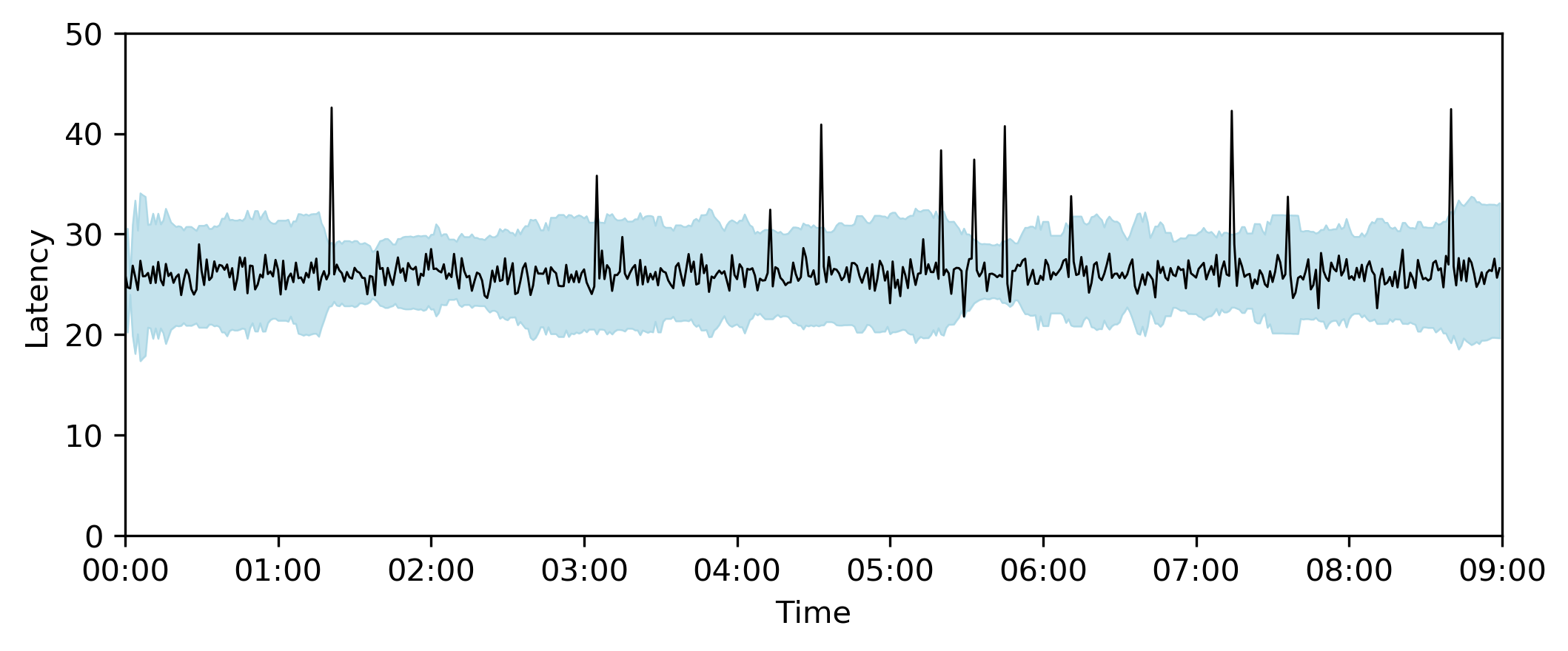
Figure 2 – The robust anomaly detector estimates the anomaly bounds (blue) at each point in time using the median and median-absolute-deviation of the target (black) over a 30-minute sliding window. Using these more robust-to-outliers statistical measures, anomaly bounds vary more smoothly over time.
This approach works well for metrics that show stationary behavior (i.e., their mean and variance do not change over time), but data often change over years and seasons, exhibiting trends and seasonality. In these cases, anomaly bounds are likely to be lagged and out of date (Figure 3). One approach is to remove the trend from the time series by taking the difference of every point with its previous point, and thus working on a time series where . This technique can be effective for seasonal data as well. Another approach is to instead fit curves with cyclical behavior to the data directly and thereby eliminate the lagging behavior.

Figure 3 – The anomaly detector estimates the anomaly bounds (blue) at each point in time using the median and median-absolute-deviation of the target (black) over a 30-minute sliding window. On this highly seasonal dataset, the anomaly bounds exhibit a lagged response.
Multi-variable anomaly detection with machine learning
In many systems, system health is determined by the value of multiple metrics. A straightforward extension of the single-metric anomaly-detection approach is to develop anomaly detectors for each metric independently, but this ignores possible correlations or cause-effect relationships between metrics. For example, we may expect to see a correlation between latency and traffic levels. A spike in network latency alone may appear anomalous but may be expected when viewed within the context of a corresponding spike in network traffic. In other words, high network latency may be anomalous only when traffic is low.
When multiple, correlated metrics determine system health, we can use machine learning approaches to identify anomalies. When data are not labeled, as is typical in the case of multi-variate anomalies (i.e., apart from obvious cases of system failure, we don’t know whether the behavior of system is anomalous or not at any point in time), unsupervised learning techniques, such as Robust Covariance, One-Class SVM, and Isolation Forests may be suitable. These algorithms essentially work by identifying groups of similar data points and considering the points outside of these groups to be anomalies. The Robust Covariance technique assumes that normal data points have a Gaussian distribution, and accordingly estimates the shape of the joint distribution (i.e., estimates the mean and covariance of the multivariate Gaussian distribution). The One-Class SVM algorithm relaxes the Gaussian assumption; instead, it identifies arbitrarily shaped regions with a high density of normal points. Isolation Forests, on the other hand, don’t make any assumptions about the shape of the distribution: a collection of decision trees is constructed, in which each individual decision tree splits data along a random point. Anomalies are considered to be the most isolated points. Figure 4 shows the performance of Robust Covariance, One-Class SVM, Isolation Forests models on several simulated datasets (unimodal, bimodal, spiral).

Figure 4 – The performance of three machine learning algorithms for anomaly detection (Robust Covariance on the left, One-Class SVM in the middle, Isolation Forest on the right) on three multivariate datasets (unimodal on top, bimodal in the middle, spiral on bottom). The normal data points are shown in orange, anomalous data points in orange, and classification boundaries in black. Orange points are normal data, blue points outliers, and the black curves draws the learned decision boundary. The Robust Covariance method exhibits elliptical boundaries, which are unable to properly classify complex shapes. The One-Class SVM method exhibits more smooth and flexible boundaries. And the Isolation Forest method exhibits abrupt, but more accurate, boundaries. Source code is from scikit-learn.org/stable/auto_examples/plot_anomaly_comparison.html.
A deep learning approach
Neural network-based autoencoders are another increasingly popular tool for multivariate anomaly detection. Autoencoders learn efficient representations of complex datasets by encoding them through an unsupervised training process, in which high-dimensional multivariate datasets are represented in lower dimensions. For example, a dataset of cat pictures may be efficiently
represented by an autoencoder, which learns to reconstruct images based on a smaller set of characteristics (e.g. the cat’s color and pose). When trained on a dataset consisting entirely of cats, the autoencoder will perform well, with low reconstruction error. When the autoencoder is faced with images of dogs, however, we expect higher reconstruction error. In a similar manner, an autoencoder trained on normal network data learns what normal behavior looks like. When normal data points are encountered, the reconstruction error is expected to be low. But when anomalous data points are encountered, the error will be high, and the datapoints will be classified as anomalies.
Next steps
Once anomaly detection models are developed, the next step is to integrate them into a production system. This can present data engineering challenges, in that anomalies should be detected in real-time, on a continuous basis, with a potentially high volume of streaming data. The anomaly detector output can then be integrated into an automatic root cause analysis system, and finally into a system for running predictive maintenance. These topics will be the subject of future blog posts.
This article has been published from the source link without modifications to the text. Only the headline has been changed.
Source link



