Introduction to Data Structures and Algorithms
Data Structure is a way of collecting and organising data in such a way that we can perform operations on these data in an effective way. Data Structures is about rendering data elements in terms of some relationship, for better organization and storage. For example, we have some data which has, player’s name “Virat” and age 26. Here “Virat” is of String data type and 26 is of integer data type.
We can organize this data as a record like Player record, which will have both player’s name and age in it. Now we can collect and store player’s records in a file or database as a data structure. For example: “Dhoni” 30, “Gambhir” 31, “Sehwag” 33
If you are aware of Object Oriented programming concepts, then a class also does the same thing, it collects different type of data under one single entity. The only difference being, data structures provides for techniques to access and manipulate data efficiently.
In simple language, Data Structures are structures programmed to store ordered data, so that various operations can be performed on it easily. It represents the knowledge of data to be organized in memory. It should be designed and implemented in such a way that it reduces the complexity and increases the efficiency.
Basic types of Data Structures
As we have discussed above, anything that can store data can be called as a data structure, hence Integer, Float, Boolean, Char etc, all are data structures. They are known as Primitive Data Structures.
Then we also have some complex Data Structures, which are used to store large and connected data. Some example of Abstract Data Structure are :
- Linked List
- Tree
- Graph
- Stack, Queue etc.
All these data structures allow us to perform different operations on data. We select these data structures based on which type of operation is required. We will look into these data structures in more details in our later lessons.
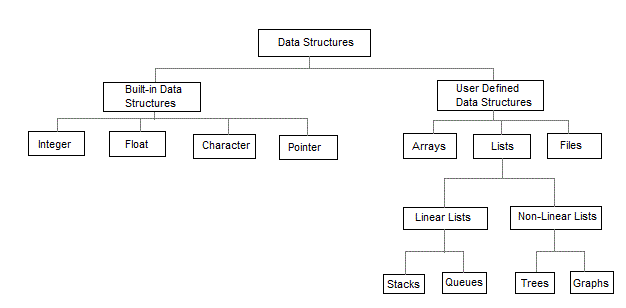
The data structures can also be classified on the basis of the following characteristics:
| Characterstic | Description |
|---|---|
| Linear | In Linear data structures,the data items are arranged in a linear sequence. Example: Array |
| Non-Linear | In Non-Linear data structures,the data items are not in sequence. Example: Tree, Graph |
| Homogeneous | In homogeneous data structures,all the elements are of same type. Example: Array |
| Non-Homogeneous | In Non-Homogeneous data structure, the elements may or may not be of the same type. Example: Structures |
| Static | Static data structures are those whose sizes and structures associated memory locations are fixed, at compile time. Example: Array |
| Dynamic | Dynamic structures are those which expands or shrinks depending upon the program need and its execution. Also, their associated memory locations changes. Example: Linked List created using pointers |
What is an Algorithm ?
An algorithm is a finite set of instructions or logic, written in order, to accomplish a certain predefined task. Algorithm is not the complete code or program, it is just the core logic(solution) of a problem, which can be expressed either as an informal high level description as pseudocode or using a flowchart.
Every Algorithm must satisfy the following properties:
- Input– There should be 0 or more inputs supplied externally to the algorithm.
- Output– There should be atleast 1 output obtained.
- Definiteness– Every step of the algorithm should be clear and well defined.
- Finiteness– The algorithm should have finite number of steps.
- Correctness– Every step of the algorithm must generate a correct output.
An algorithm is said to be efficient and fast, if it takes less time to execute and consumes less memory space. The performance of an algorithm is measured on the basis of following properties :
- Time Complexity
- Space Complexity
Space Complexity
Its the amount of memory space required by the algorithm, during the course of its execution. Space complexity must be taken seriously for multi-user systems and in situations where limited memory is available.
An algorithm generally requires space for following components :
- Instruction Space: Its the space required to store the executable version of the program. This space is fixed, but varies depending upon the number of lines of code in the program.
- Data Space: Its the space required to store all the constants and variables(including temporary variables) value.
- Environment Space: Its the space required to store the environment information needed to resume the suspended function.
To learn about Space Complexity in detail, jump to the Space Complexity tutorial.
Time Complexity
Time Complexity is a way to represent the amount of time required by the program to run till its completion. It’s generally a good practice to try to keep the time required minimum, so that our algorithm completes it’s execution in the minimum time possible. We will study about Time Complexity in details in later sections.
NOTE: Before going deep into data structure, you should have a good knowledge of programming either in C or in C++ or Java or Python etc.
Asymptotic Notations
When it comes to analysing the complexity of any algorithm in terms of time and space, we can never provide an exact number to define the time required and the space required by the algorithm, instead we express it using some standard notations, also known as Asymptotic Notations.
When we analyse any algorithm, we generally get a formula to represent the amount of time required for execution or the time required by the computer to run the lines of code of the algorithm, number of memory accesses, number of comparisons, temporary variables occupying memory space etc. This formula often contains unimportant details that don’t really tell us anything about the running time.
Let us take an example, if some algorithm has a time complexity of T(n) = (n2 + 3n + 4), which is a quadratic equation. For large values of n, the 3n + 4 part will become insignificant compared to the n2 part.
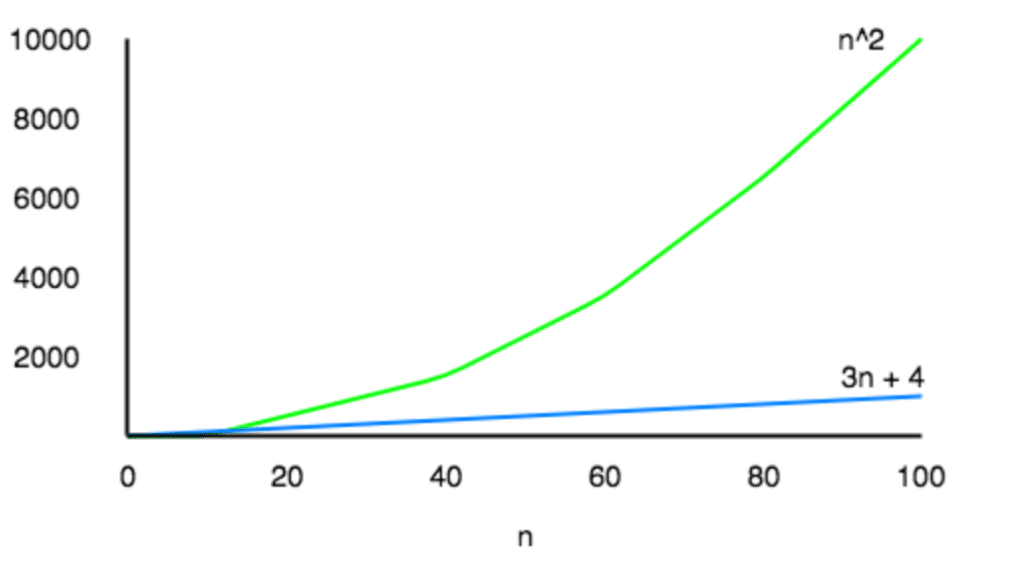
For n = 1000, n2 will be 1000000 while 3n + 4 will be 3004.
Also, When we compare the execution times of two algorithms the constant coefficients of higher order terms are also neglected.
An algorithm that takes a time of 200n2 will be faster than some other algorithm that takes n3 time, for any value of n larger than 200. Since we’re only interested in the asymptotic behavior of the growth of the function, the constant factor can be ignored too.
What is Asymptotic Behaviour
The word Asymptotic means approaching a value or curve arbitrarily closely (i.e., as some sort of limit is taken).
Remember studying about Limits in High School, this is the same.
The only difference being, here we do not have to find the value of any expression where n is approaching any finite number or infinity, but in case of Asymptotic notations, we use the same model to ignore the constant factors and insignificant parts of an expression, to device a better way of representing complexities of algorithms, in a single coefficient, so that comparison between algorithms can be done easily.
Let’s take an example to understand this:
If we have two algorithms with the following expressions representing the time required by them for execution, then:
Expression 1: (20n2 + 3n – 4)
Expression 2: (n3 + 100n – 2)
Now, as per asymptotic notations, we should just worry about how the function will grow as the value of n(input) will grow, and that will entirely depend on n2 for the Expression 1, and on n3 for Expression 2. Hence, we can clearly say that the algorithm for which running time is represented by the Expression 2, will grow faster than the other one, simply by analysing the highest power coeeficient and ignoring the other constants(20 in 20n2) and insignificant parts of the expression(3n - 4 and 100n - 2).
The main idea behind casting aside the less important part is to make things manageable.
All we need to do is, first analyse the algorithm to find out an expression to define it’s time requirements and then analyse how that expression will grow as the input(n) will grow.
Types of Asymptotic Notations
We use three types of asymptotic notations to represent the growth of any algorithm, as input increases:
- Big Theta (Θ)
- Big Oh(O)
- Big Omega (Ω)
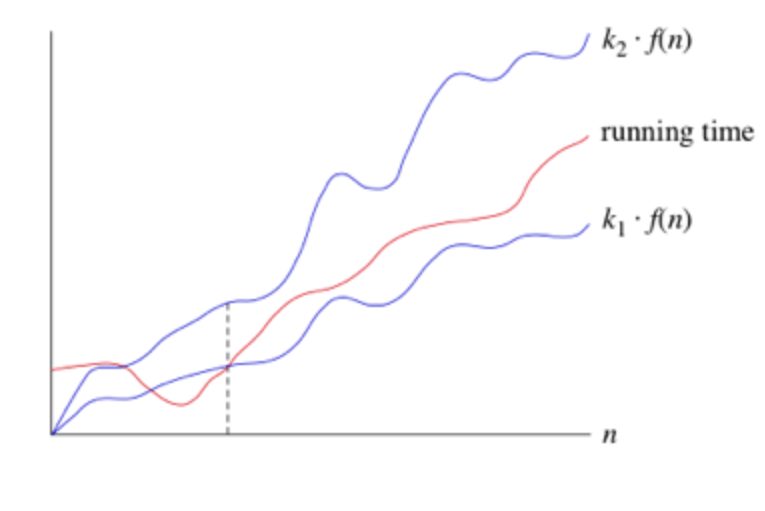
Tight Bounds: Theta
When we say tight bounds, we mean that the time compexity represented by the Big-Θ notation is like the average value or range within which the actual time of execution of the algorithm will be.
For example, if for some algorithm the time complexity is represented by the expression 3n2 + 5n, and we use the Big-Θ notation to represent this, then the time complexity would be Θ(n2), ignoring the constant coefficient and removing the insignificant part, which is 5n.
Here, in the example above, complexity of Θ(n2) means, that the avaerage time for any input n will remain in between, k1 * n2 and k2 * n2, where k1, k2 are two constants, therby tightly binding the expression rpresenting the growth of the algorithm.
Upper Bounds: Big-O
This notation is known as the upper bound of the algorithm, or a Worst Case of an algorithm.
It tells us that a certain function will never exceed a specified time for any value of input n.
The question is why we need this representation when we already have the big-Θ notation, which represents the tightly bound running time for any algorithm. Let’s take a small example to understand this.
Consider Linear Search algorithm, in which we traverse an array elements, one by one to search a given number.
In Worst case, starting from the front of the array, we find the element or number we are searching for at the end, which will lead to a time complexity of n, where n represents the number of total elements.
But it can happen, that the element that we are searching for is the first element of the array, in which case the time complexity will be 1.
Now in this case, saying that the big-Θ or tight bound time complexity for Linear search is Θ(n), will mean that the time required will always be related to n, as this is the right way to represent the average time complexity, but when we use the big-O notation, we mean to say that the time complexity is O(n), which means that the time complexity will never exceed n, defining the upper bound, hence saying that it can be less than or equal to n, which is the correct representation.
This is the reason, most of the time you will see Big-O notation being used to represent the time complexity of any algorithm, because it makes more sense.
Lower Bounds: Omega
Big Omega notation is used to define the lower bound of any algorithm or we can say the best case of any algorithm.
This always indicates the minimum time required for any algorithm for all input values, therefore the best case of any algorithm.
In simple words, when we represent a time complexity for any algorithm in the form of big-Ω, we mean that the algorithm will take atleast this much time to cmplete it’s execution. It can definitely take more time than this too.
Space Complexity of Algorithms
Whenever a solution to a problem is written some memory is required to complete. For any algorithm memory may be used for the following:
- Variables (This include the constant values, temporary values)
- Program Instruction
- Execution
Space complexity is the amount of memory used by the algorithm (including the input values to the algorithm) to execute and produce the result.
Sometime Auxiliary Space is confused with Space Complexity. But Auxiliary Space is the extra space or the temporary space used by the algorithm during it’s execution.
Space Complexity = Auxiliary Space + Input space
Memory Usage while Execution
While executing, algorithm uses memory space for three reasons:
- Instruction SpaceIt’s the amount of memory used to save the compiled version of instructions.
- Environmental StackSometimes an algorithm(function) may be called inside another algorithm(function). In such a situation, the current variables are pushed onto the system stack, where they wait for further execution and then the call to the inside algorithm(function) is made.For example, If a function
A()calls functionB()inside it, then all th variables of the functionA()will get stored on the system stack temporarily, while the functionB()is called and executed inside the funcitonA(). - Data SpaceAmount of space used by the variables and constants.
But while calculating the Space Complexity of any algorithm, we usually consider only Data Space and we neglect the Instruction Space and Environmental Stack.
Calculating the Space Complexity
For calculating the space complexity, we need to know the value of memory used by different type of datatype variables, which generally varies for different operating systems, but the method for calculating the space complexity remains the same.
| Type | Size |
|---|---|
| bool, char, unsigned char, signed char, __int8 | 1 byte |
| __int16, short, unsigned short, wchar_t, __wchar_t | 2 bytes |
| float, __int32, int, unsigned int, long, unsigned long | 4 bytes |
| double, __int64, long double, long long | 8 bytes |
Now let’s learn how to compute space complexity by taking a few examples:
{
int z = a + b + c;
return(z);
}In the above expression, variables a, b, c and z are all integer types, hence they will take up 4 bytes each, so total memory requirement will be (4(4) + 4) = 20 bytes, this additional 4 bytes is for return value. And because this space requirement is fixed for the above example, hence it is called Constant Space Complexity.
Let’s have another example, this time a bit complex one,
// n is the length of array a[]
int sum(int a[], int n)
{
int x = 0; // 4 bytes for x
for(int i = 0; i < n; i++) // 4 bytes for i
{
x = x + a[i];
}
return(x);
}- In the above code,
4*nbytes of space is required for the arraya[]elements. - 4 bytes each for
x,n,iand the return value.
Hence the total memory requirement will be (4n + 12), which is increasing linearly with the increase in the input value n, hence it is called as Linear Space Complexity.
Similarly, we can have quadratic and other complex space complexity as well, as the complexity of an algorithm increases.
But we should always focus on writing algorithm code in such a way that we keep the space complexity minimum.
Time Complexity of Algorithms
For any defined problem, there can be N number of solution. This is true in general. If I have a problem and I discuss about the problem with all of my friends, they will all suggest me different solutions. And I am the one who has to decide which solution is the best based on the circumstances.
Similarly for any problem which must be solved using a program, there can be infinite number of solutions. Let’s take a simple example to understand this. Below we have two different algorithms to find square of a number(for some time, forget that square of any number n is n*n):
One solution to this problem can be, running a loop for n times, starting with the number n and adding n to it, every time.
/*
we have to calculate the square of n
*/
for i=1 to n
do n = n + n
// when the loop ends n will hold its square
return nOr, we can simply use a mathematical operator * to find the square.
/*
we have to calculate the square of n
*/
return n*nIn the above two simple algorithms, you saw how a single problem can have many solutions. While the first solution required a loop which will execute for n number of times, the second solution used a mathematical operator * to return the result in one line. So which one is the better approach, of course the second one.
What is Time Complexity?
Time complexity of an algorithm signifies the total time required by the program to run till its completion.
The time complexity of algorithms is most commonly expressed using the big O notation. It’s an asymptotic notation to represent the time complexity. We will study about it in detail in the next tutorial.
Time Complexity is most commonly estimated by counting the number of elementary steps performed by any algorithm to finish execution. Like in the example above, for the first code the loop will run n number of times, so the time complexity will be n atleast and as the value of n will increase the time taken will also increase. While for the second code, time complexity is constant, because it will never be dependent on the value of n, it will always give the result in 1 step.
And since the algorithm’s performance may vary with different types of input data, hence for an algorithm we usually use the worst-case Time complexity of an algorithm because that is the maximum time taken for any input size.
Calculating Time Complexity
Now lets tap onto the next big topic related to Time complexity, which is How to Calculate Time Complexity. It becomes very confusing some times, but we will try to explain it in the simplest way.
Now the most common metric for calculating time complexity is Big O notation. This removes all constant factors so that the running time can be estimated in relation to N, as N approaches infinity. In general you can think of it like this :
statement;
Above we have a single statement. Its Time Complexity will be Constant. The running time of the statement will not change in relation to N.
for(i=0; i < N; i++)
{
statement;
}The time complexity for the above algorithm will be Linear. The running time of the loop is directly proportional to N. When N doubles, so does the running time.
for(i=0; i < N; i++)
{
for(j=0; j < N;j++)
{
statement;
}
}This time, the time complexity for the above code will be Quadratic. The running time of the two loops is proportional to the square of N. When N doubles, the running time increases by N * N.
while(low <= high)
{
mid = (low + high) / 2;
if (target < list[mid])
high = mid - 1;
else if (target > list[mid])
low = mid + 1;
else break;
}This is an algorithm to break a set of numbers into halves, to search a particular field(we will study this in detail later). Now, this algorithm will have a Logarithmic Time Complexity. The running time of the algorithm is proportional to the number of times N can be divided by 2(N is high-low here). This is because the algorithm divides the working area in half with each iteration.
void quicksort(int list[], int left, int right)
{
int pivot = partition(list, left, right);
quicksort(list, left, pivot - 1);
quicksort(list, pivot + 1, right);
}Taking the previous algorithm forward, above we have a small logic of Quick Sort(we will study this in detail later). Now in Quick Sort, we divide the list into halves every time, but we repeat the iteration N times(where N is the size of list). Hence time complexity will be N*log( N ). The running time consists of N loops (iterative or recursive) that are logarithmic, thus the algorithm is a combination of linear and logarithmic.
NOTE: In general, doing something with every item in one dimension is linear, doing something with every item in two dimensions is quadratic, and dividing the working area in half is logarithmic.
Types of Notations for Time Complexity
Now we will discuss and understand the various notations used for Time Complexity.
- Big Oh denotes “fewer than or the same as” <expression> iterations.
- Big Omega denotes “more than or the same as” <expression> iterations.
- Big Theta denotes “the same as” <expression> iterations.
- Little Oh denotes “fewer than” <expression> iterations.
- Little Omega denotes “more than” <expression> iterations.
Understanding Notations of Time Complexity with Example
O(expression) is the set of functions that grow slower than or at the same rate as expression. It indicates the maximum required by an algorithm for all input values. It represents the worst case of an algorithm’s time complexity.
Omega(expression) is the set of functions that grow faster than or at the same rate as expression. It indicates the minimum time required by an algorithm for all input values. It represents the best case of an algorithm’s time complexity.
Theta(expression) consist of all the functions that lie in both O(expression) and Omega(expression). It indicates the average bound of an algorithm. It represents the average case of an algorithm’s time complexity.
Suppose you’ve calculated that an algorithm takes f(n) operations, where,
f(n) = 3*n^2 + 2*n + 4. // n^2 means square of nSince this polynomial grows at the same rate as n2, then you could say that the function f lies in the set Theta(n2). (It also lies in the sets O(n2) and Omega(n2) for the same reason.)
The simplest explanation is, because Theta denotes the same as the expression. Hence, as f(n) grows by a factor of n2, the time complexity can be best represented as Theta(n2).
This article has been published from the source link without modifications to the text. Only the headline has been changed.













