Introduction
Ownership of bitcoin is established through digital keys, bitcoin addresses and digital signatures. The digital keys are not actually stored in the network, but are instead created and stored by end-users in a file, or simple database, called a wallet. The digital keys in a user’s wallet are completely independent of the bitcoin protocol and can be generated and managed by the user’s wallet software without reference to the blockchain or access to the Internet. Keys enable many of the interesting properties of bitcoin, including decentralized trust and control, ownership attestation and the cryptographic-proof secu‐ rity model.
HNFUzKACoVNLnyx4PlW7hJg3dpko2UlDwttaxaU‐ Pan4afMmK9ZAtHMKB4PqJgYFe8VDIp0x7OpruTFugxA5hBTE=
Every bitcoin transaction requires a valid signature to be included in the blockchain, which can only be generated with valid digital keys, therefore anyone with a copy of those keys has control of the bitcoin in that account. Keys come in pairs consisting of a private (secret) and public key. Think of the public key as similar to a bank account number and the private key as similar to the secret PIN number, or signature on a cheque that provides control over the account. These digital keys are very rarely seen by the users of bitcoin. For the most part, they are stored inside the wallet file and managed by the bitcoin wallet software.
In this chapter we will introduce wallets, which contain cryptographic keys. We will look at how keys are generated, stored and managed. We will review the various en‐ coding formats used to represent private and public keys, addresses and script addresses. Finally we will look at special uses of keys: to sign messages, to prove ownership and to create vanity addresses and paper wallets.
Public key cryptography and crypto-currency
Public key cryptography was invented in the 1970s and is a mathematical foundation for computer and information security.
Since the invention of public key cryptography, several suitable mathematical functions, such as prime number exponentiation and elliptic curve multiplication, have been dis‐ covered. These mathematical functions are practically irreversible, meaning that they are easy to calculate in one direction and infeasible to calculate in the opposite direction. Based on these mathematical functions, cryptography enables the creation of digital secrets and unforgeable digital signatures. Bitcoin uses elliptic curve multiplication as the basis for its public key cryptography.
In bitcoin, we use public key cryptography to create a key pair that controls access to bitcoins. The key pair consists of a private key and — derived from it — a unique public key. The public key is used to receive bitcoins, and the private key is used to sign trans‐ actions to spend those bitcoins.
There is a mathematical relationship between the public and the private key that allows the private key to be used to generate signatures on messages. This signature can be validated against the public key without revealing the private key.
When spending bitcoins, the current bitcoin owner presents their public key and a signature (different each time, but created from the same private key; see (to come)) in a transaction to spend those bitcoins. Through the presentation of the public key and signature everyone in the bitcoin network can verify and accept the transaction as valid, confirming that the person transferring the bitcoins owned them at the time of the transfer.
In most wallet implementations, the private and public keys are stor‐ ed together as a key pair for convenience. However, the public key can be calculated from the private key, so storing only the private key is also possible.
Private and Public Keys
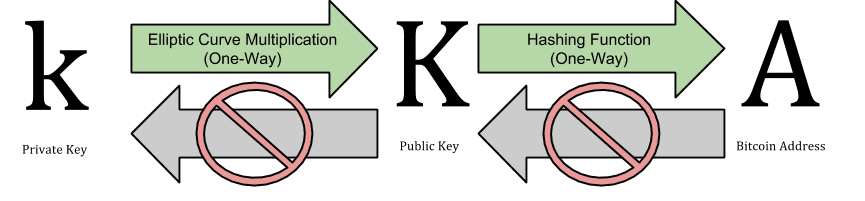
A bitcoin wallet contains a collection of key pairs, each consisting of a private key and a public key. The private key (k) is a number, usually picked at random. From the private key, we use elliptic curve multiplication, a one-way cryptographic function, to generate a public key (K). From the public key (K), we use a one-way cryptographic hash function to generate a bitcoin address (A). In this section we will start with generating the private key, look at the elliptic curve math that is used to turn that into a public key, and finally, generate a bitcoin address from the public key. The relationship between private key, public key and bitcoin address is shown below:
Private Keys
A private key is simply a number, picked at random. Ownership and control over the private key is the root of user control over all funds associated with the corresponding bitcoin address. The private key is used to create signatures that are required to spend bitcoins by proving ownership of funds used in a transaction. The private key must remain secret at all times, as revealing it to a third party is equivalent to giving them control over the bitcoins secured by that key. The private key must also be backed up and protected from accidental loss, since if lost it cannot be recovered and the funds secured by it are forever lost too.
The bitcoin private key is just a number. You can pick your private keys randomly using just a coin, pencil and paper: Toss a coin 256 times and you have the binary digits of a random private key you can use in a bitcoin wallet. The public key can be then generated from the private key.
Generating a private key from a random number
The first and most important step in generating keys is to find a secure source of entropy, or randomness. Creating a bitcoin key is essentially the same as “Pick a number between 1 and 2^256“. The exact method you use to pick that number does not matter as long as it is not predictable or repeatable. Bitcoin software uses the underlying operating system’s random number generators to produce 256 bits of entropy (randomness). Usually, the OS random number generator is initialized by a human source of randomness, which is why you may be asked to wiggle your mouse around for a few seconds. For the truly paranoid, nothing beats dice, pencil and paper.
More accurately, the private key can be any number between 1 and n – 1, where n is a constant (n = 1.158 * 10^77, slightly less than 2^256) defined as the order of the elliptic curve used in bitcoin. To create such a key, we randomly pick a 256-bit number and check that it is less than n – 1. In programming terms, this is usually achieved by feeding a larger string of random bits, collected from a cryptographically-secure source of randomness, into the SHA-256 hash algorithm which will conveniently produce a 256-bit number. If the result is less than n – 1, we have a suitable private key. Otherwise, we simply try again with another random number.
Do not write your own code to create a random number or use a “simple” random number generator offered by your programming language. Use a cryptographically-secure pseudo-random number generator (CSPRNG) with a seed from a source of sufficient entro‐ py. Study the documentation of the random number generator li‐ brary you choose to make sure it is cryptographically secure. Cor‐ rect implementation of the CSPRNG is critical to the security of the keys.
Below is a randomly generated private key shown in hexadecimal format (256 binary digits shown as 64 hexadecimal digits, each 4 bits):
Randomly generated private key (k).
1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDD
The size of bitcoin’s private key space, 2^256 is an unfathomably large number. It is approximately 10^77 in decimal. The visible universe is estimated to contain 10^80 atoms.
To generate a new key with the Bitcoin Core Client, use the getnewad dress command. For security reasons it displays the public key only, not the private key. To ask bitcoind to expose the private key, use the dumpprivkey command. The dumpprivkey shows the private key in a base-58 checksum encoded format called the Wallet Import Format (WIF).
Here’s an example of generating and displaying a private key using these two commands:
$ bitcoind getnewaddress
1J7mdg5rbQyUHENYdx39WVWK7fsLpEoXZy
$ bitcoind dumpprivkey 1J7mdg5rbQyUHENYdx39WVWK7fsLpEoXZy
KxFC1jmwwCoACiCAWZ3eXa96mBM6tb3TYzGmf6YwgdGWZgawvrtJ
The dumpprivkey command opens the wallet and extracts the private key that was gen‐ erated by the getnewaddress command. It is not otherwise possible for bitcoind to know the private key from the public key, unless they are both stored in the wallet.
You can also use the command-line sx tools to generate and display private keys:
New key with sx tools
$ sx newkey 5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2JpbnkeyhfsYB1Jcn
Public Keys
The public key is calculated from the private key using elliptic curve multiplication, which is irreversible: K = k *G where k is the private key, G is a constant point called the Generator Point and K is the resulting public key. The reverse operation, known as “finding the discrete logarithm” — calculating k if you know K — is as difficult as trying all possible values of k, i.e., a brute-force search. Before we demonstrate how to generate a public key from a private key, let’s look at Elliptic Curve Cryptography in a bit more detail.
Elliptic Curve Cryptography Explained
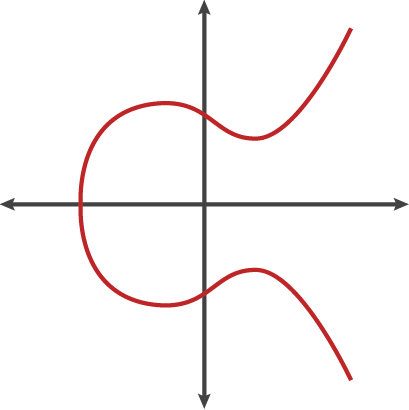
Elliptic Curve Cryptography is a type of asymmetric or public-key cryptography based on the discrete logarithm problem as expressed by addition and multiplication on the points of an elliptic curve.
Below we see an example of an elliptic curve, similar to that used by bitcoin:
Bitcoin uses a specific elliptic curve and set of mathematical constants, as defined in a standard called secp256k1, established by the National Institute of Standards and Tech‐ nology (NIST). The secp256k1 curve is defined by the following function, which pro‐ duces an elliptic curve:
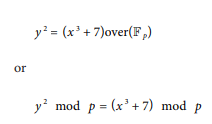
The mod p (modulo prime number p) indicates that this curve is over a finite field of prime order p, also written as ኀp , where p = 2^256 – 2^32 – 2^9 – 2^8 – 2^7 – 2^6 – 2^4 – 1, a very large prime number.
Because this curve is defined over a finite field of prime order instead of over the real numbers it looks like a pattern of dots scattered in two dimensions, which makes it difficult to visualize. However, the math is identical as that of an elliptic curve over the real numbers shown above. As an example, below is the same elliptic curve over a much smaller finite field of prime order 17, showing a pattern of dots on a grid. The secp256k1 bitcoin elliptic curve can be thought of as a much more complex pattern of dots on a unfathomably large grid.
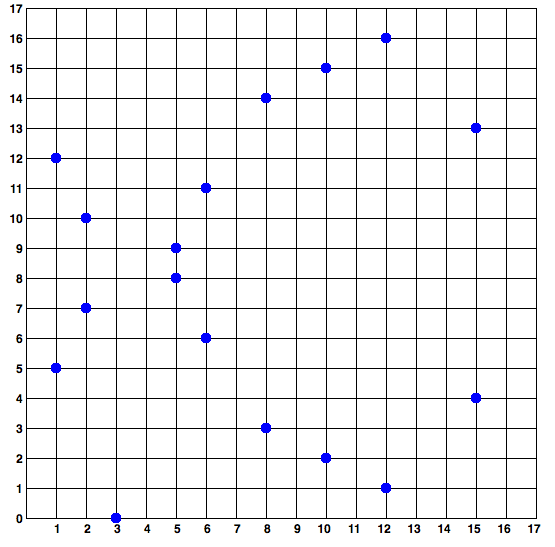
So for example, below is a point P with coordinates (x,y) that is a point on the secp256k1 curve. You can check this yourself using Python:
P = (55066263022277343669578718895168534326250603453777594175500187360389116729240,\ 32670510020758816978083085130507043184471273380659243275938904335757337482424)
Python 3.4.0 (default, Mar 30 2014, 19:23:13)
[GCC 4.2.1 Compatible Apple LLVM 5.1 (clang-503.0.38)] on darwin
Type "help", "copyright", "credits" or "license" for more information.
>>> p = 115792089237316195423570985008687907853269984665640564039457584007908834671663
>>> x = 55066263022277343669578718895168534326250603453777594175500187360389116729240
>>> y = 32670510020758816978083085130507043184471273380659243275938904335757337482424
>>> (x ** 3 + 7 - y**2) % p
0In elliptic curve math, there is a point called the “point at infinity”, which roughly cor‐ responds to the role of 0 in addition. On computers, it’s sometimes represented by x = y = 0 (which doesn’t satisfy the elliptic curve equation — but it’s an easy separate case that can be checked).
There is also an operator “+”, called “addition” which has some properties similar to the traditional addition of real numbers that grade school children learn. Given two points P1 and P2 on the elliptic curve, there is a third point P3 = P1 + P2 , also on the elliptic curve.
Geometrically, this third point P3 is calculated by drawing a line between P1 and P2 . This line will intersect the elliptic curve in exactly one additional place. Call this point P3 ‘ = (x, y). Then reflect in the X axis to get P3 = (x, -y).
There are a couple of special cases which explain the need for the “point at infinity”
If P1 and P2 are the same point, the line “between” P1 and P2 should extend to be the tangent on the curve at this point P1 . This tangent will intersect the curve in exactly one new point. You can use techniques from calculus to determine the slope of the tangent line. These techniques curiously work even though we are restricting our interest to points on the curve with two integer coordinates!
In some cases (i.e., if P1 and P2 have the same x values but different y values), the tangent line will be exactly vertical, in which case P3 = “point at infinity”.
If P1 is the “point at infinity”, then the sum P1 + P2 = P2 . Similary, if P2 is the point at infinity, then P1 + P2 = P1 . This shows how the point at infinity plays the roll of 0.
It turns out that + is associative, which means that (A+B)+C = A+(B+C). That means we can write A+B+C without parentheses without any ambiguity.
Now that we have defined addition, we can define multiplication in the standard way that extends addition. For a point P on the elliptic curve, if k is a whole number, then kP = P + P + P + … + P (k times). Note that k is sometimes confusingly called an “exponent” in this case.
Generating a public key
Starting with a private key in the form of a randomly generated number k, we multiply it by a predetermined point on the curve called the generator point G to produce another point somewhere else on the curve, which is the corresponding public key K. The gen‐ erator point is specified as part of the secp256k1 standard and is always the same for all keys in bitcoin.
K = k *G
where k is the private key, G is the generator point, and K is the resulting public key, a point on the curve. Since the generator point is always the same for all bitcoin users, a private key k multiplied with G will always result in the same public key K. The rela‐ tionship between k and K is fixed, but can only be calculated in one direction, from k to K. That’s why a bitcoin address (derived from K) can be shared with anyone and does not reveal the user’s private key (k).
A private key can be converted into a public key, but a public key cannot be converted back into a private key because the math only works one way.
Implementing the elliptic curve multiplication above, we take the private key generated previously and multiply it by G:
Multiply the private key k with the generator point G to find the public key K.
K = 1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDD * G
Public Key K defined as a point K = (x,y).
K = (x, y) where, x = F028892BAD...DC341A y = 07CF33DA18...505BDB
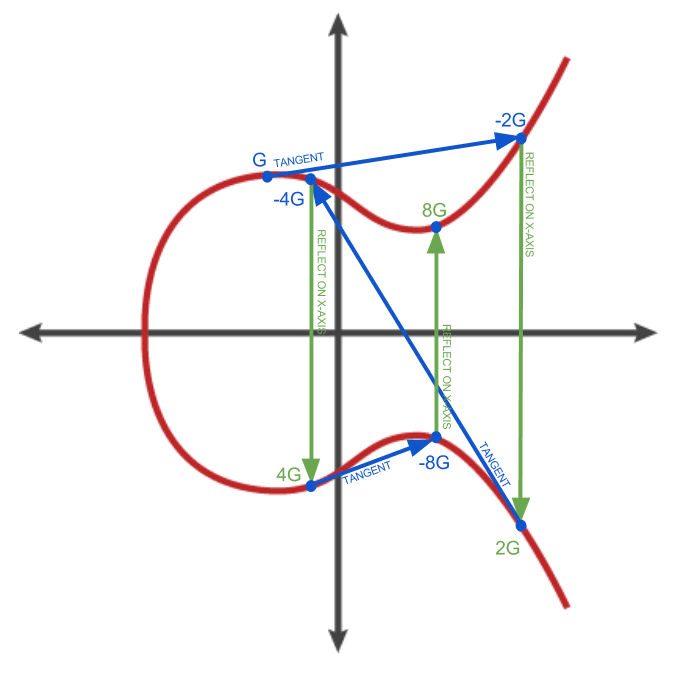
To visualize multiplication of a point with an integer, we will use the simpler elliptic curve over the real numbers — remember, the math is the same. Our goal is to find the multiple kG of the generator point G. That is the same as adding G to itself, k times in a row. In elliptic curves, adding a point to itself is the equivalent of drawing a tangent line on the point and finding where it intersects the curve again, then reflecting that point on the x-axis.
The diagram below shows the process for deriving G, 2G, 4G, as a geometric operation on the curve.
Most bitcoin implementations use the OpenSSL cryptographic li‐ brary to do the elliptic curve math. For example, to derive the pub‐ lic key, the function EC_POINT_mul() is used. See https://wiki.openssl.org/index.php/Elliptic_Curve_Cryptography
This article has been published from the source link without modifications to the text. Only the headline has been changed.