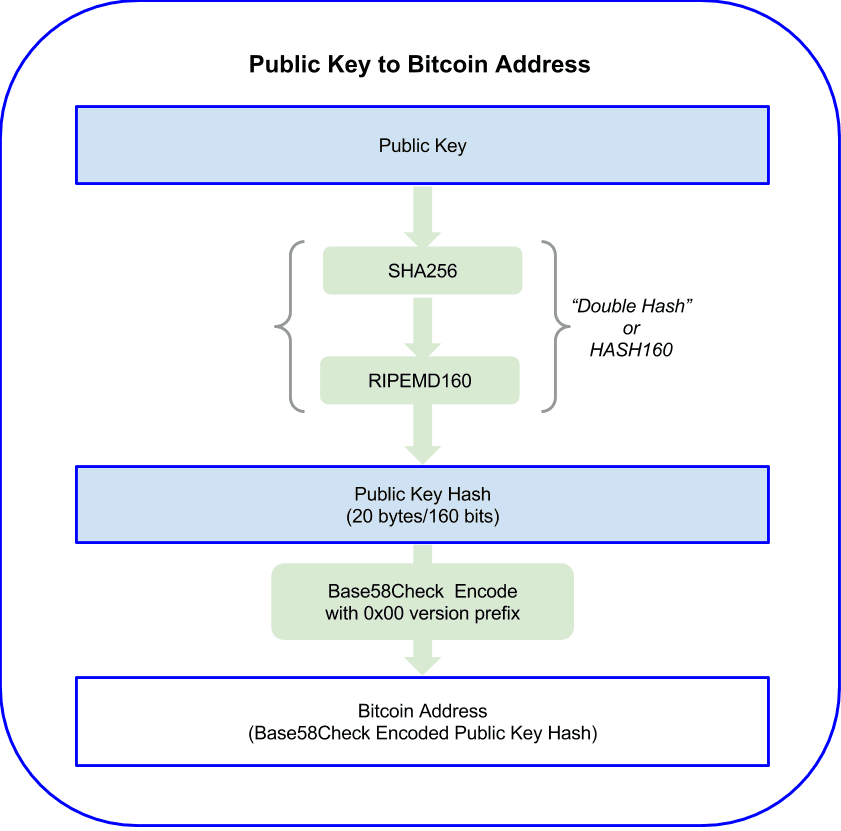
A bitcoin address is a string of digits and characters that can be shared with anyone who wants to send you money. Addresses produced from public keys consist of a string of numbers and letters, beginning with the digit “1”. Here’s an example of a bitcoin address:
1thMirt546nngXqyPEz532S8fLwbozud8
The bitcoin address is what appears most commonly in a transaction as the “recipient” of the funds. If we were to compare a bitcoin transaction to a paper cheque, the bitcoin address is the beneficiary, which is what we write on the line after “Pay to the order of ”. On a paper cheque, that beneficiary can sometimes be the name of a bank account holder, but can also include corporations, institutions or even cash. Because paper che‐ ques do not need to specify an account, but rather use an abstract name as the recipient of funds, that makes paper cheques very flexible as payment instruments. Bitcoin trans‐ actions use a similar abstraction, the bitcoin address, to make them very flexible. A bitcoin address can represent the owner of a private/public key pair, or it can represent something else, such as a payment script. Let’s examine the simple case, a bitcoin address that rep‐ resents, and is derived from, a public key.
The bitcoin address is derived from the public key through the use of one-way crypto‐ graphic hashing; a “hashing algorithm” or simply “hash algorithm” is a one-way function that produces a fingerprint or “hash” of an arbitrary sized input. Cryptographic hash functions are used extensively in bitcoin: in bitcoin addresses, in script addresses and in the mining “Proof-of-Work” algorithm. The algorithms used to make a bitcoin ad‐ dress from a public key are the Secure Hash Algorithm (SHA) and the RACE Integrity Primitives Evaluation Message Digest (RIPEMD), specifically SHA256 and RI‐ PEMD160.
Starting with the public key K, we compute the SHA256 hash and then compute the RIPEMD160 hash of the result, producing a 160 bit (20 byte) number:
A = RIPEMD160(SHA256(K))
where K is the public key and A is the resulting bitcoin address.
A bitcoin address is not the same as a public key. Bitcoin addresses are derived from a public key using a one-way function.
Bitcoin addresses are almost always presented to users in an encoding called “Base58Check” (see “Base58Check Encoding” below), which uses 58 charac‐ ters (a base-58 number system) and a checksum to help human readability, avoid am‐ biguity and protect against errors in address transcription and entry. Base58Check is also used in many other ways in bitcoin, whenever there is a need for a user to read and correctly transcribe a number, such as a bitcoin address, a private key, an encrypted key, or a script hash. In the next section we will examine the mechanics of Base58Check encoding and decoding, and the resulting representations.
Base58 and Base58Check Encoding
Base-58 Encoding
In order to represent long numbers in a compact way, using fewer symbols, many com‐ puter systems use mixed-alphanumeric representations with a base (or radix) higher than 10. For example, whereas the traditional decimal system uses the ten numerals 0 through 9, the hexadecimal system uses sixteen, with the letters A through F as the six additional symbols. A number represented in hexadecimal format is shorter than the equivalent decimal representation. Even more compact, Base-64 representation uses 26 lower case letters, 26 capital letters, 10 numerals and two more characters such as “+” and “/” to transmit binary data over text-based media such as email. Base-64 is most commonly used to add binary attachments to email. Base-58 is a text-based binaryencoding format developed for use in bitcoin and used in many other crypto-currencies. It offers a balance between compact representation, readability and error detection and prevention. Base-58 is a subset of Base-64, using the upper and lower case letters and numbers but omitting some characters that are frequently mistaken for one another and can appear identical when displayed in certain fonts. Specifically, Base-58 is Base-64 without the 0 (number zero), O (capital o), l (lower L), I (capital i) and the symbols “\ +” and “/”. Or, more simply, it is a set of lower and capital letters and numbers without the four (0, O, l, I) mentioned above.
Bitcoin’s Base-58 Alphabet.
123456789ABCDEFGHJKLMNPQRSTUVWXYZabcdefghijkmnopqrstuvwxyz
Base58Check Encoding
To add extra security against typos or transcription errors, Base58Check is a Base-58 encoding format, frequently used in bitcoin, which has a built-in error-checking code. The checksum is an additional four bytes added to the end of the data that is being encoded. The checksum is derived from the hash of the encoded data and can therefore be used to detect and prevent transcription and typing errors. When presented with a Base58Check code, the decoding software will calculate the checksum of the data and compare it to the checksum included in the code. If the two do not match, that indicates that an error has been introduced and the Base58Check data is invalid. For example, this prevents a mistyped bitcoin address from being accepted by the wallet software as a valid destination, an error which would otherwise result in loss of funds.
To convert data (a number) into a Base58Check format, we first add a prefix to the data, called the “version byte”, which serves to easily identify the type of data that is encoded. For example, in the case of a bitcoin address the prefix is zero (0x00 in hex), whereas the prefix used when encoding a private key is 128 (0x80 in hex). A list of common version prefixes is shown below in Table.
Next compute the “double-SHA” checksum, meaning we apply the SHA256 hashalgorithm twice on the previous result (prefix and data):
checksum = SHA256(SHA256(prefix+data))
From the resulting 32-byte hash (hash-of-a-hash), we take only the first four bytes. These four bytes serve as the error-checking code, or checksum. The checksum is con‐ catenated (appended) to the end.
The result of the above is now a prefix, the data and a checksum. This result is encoded using the base-58 alphabet described in the section above.
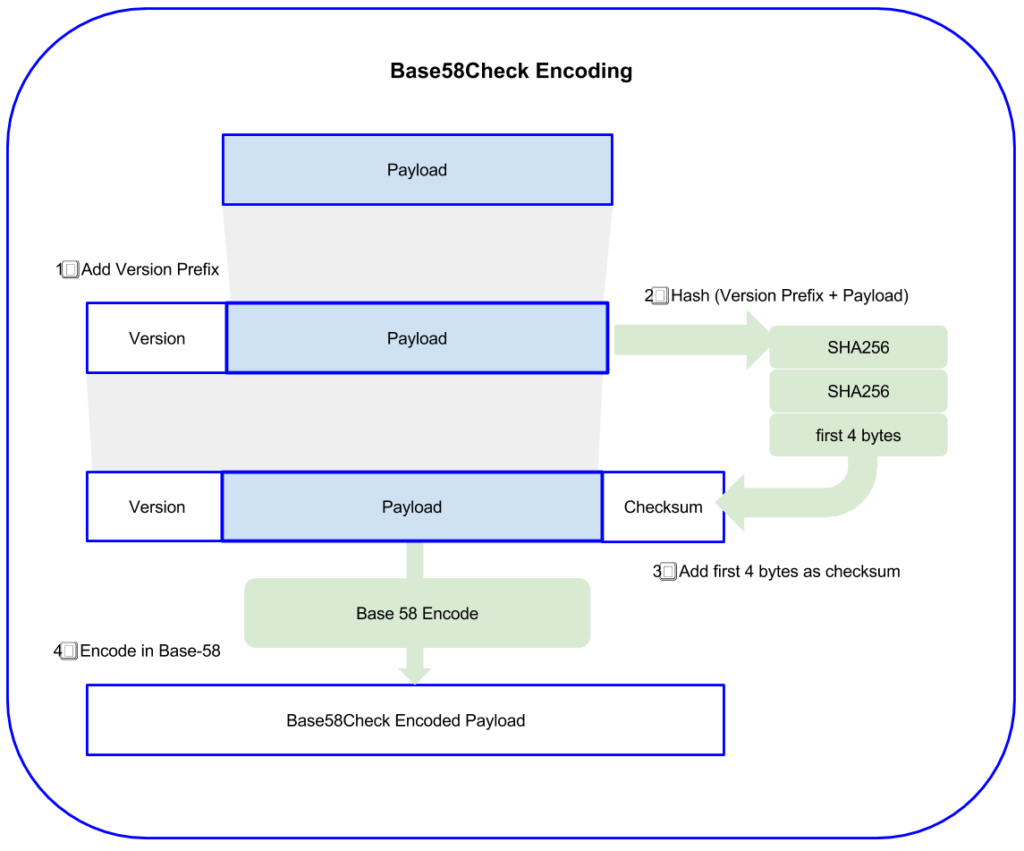
In bitcoin, most of the data presented to the user is Base58Check encoded to make it compact, easy to read and easy to detect errors. The version prefix in Base58Check encoding is used to create easily distinguishable formats, which when encoded in Base-58 contain specific characters at the beginning of the Base58Check encoded pay‐ load, making it easy for humans to identify the type of data that is encoded and how to use it. This is what differentiates, for example, a Base58Check encoded bitcoin address that starts with a “1” from a Base58Check encoded private key WIF format that starts with a “5”. Some example version prefixes and the resulting Base-58 characters are shown below:
Table – Base58Check Version Prefix and Encoded Result Examples
| Type | Version prefix (hex) | Base-58 result prefix |
| Bitcoin Address Pay-to-Script-Hash Address Bitcoin Testnet Address Private Key WIF BIP38 Encrypted Private Key BIP32 Extended Public Key |
0x00 0x05 0x6F 0x80 0x0142 0x0488B21E |
1 3 m or n 5, K or L 6P xpub |
Creating a bitcoin address from a private key
Let’s look at the complete process of creating a bitcoin address, from a private key, to a public key (a point on the elliptic curve), to a double-hashed address and finally the Base58Check encoding. The C++ code in Example 4-1 shows the complete process, from private key, to Base58Check encoded bitcoin address, step-by-step. The code ex‐ ample uses the libbitcoin library introduced in “Alternative clients, libraries and tool‐ kits” on page 56 for some helper functions:
Example – Creating a Base58Check encoded bitcoin address from a private key
#include <bitcoin/bitcoin.hpp>
int main()
{
// Private secret key.
bc::ec_secret secret = bc::decode_hash(
"038109007313a5807b2eccc082c8c3fbb988a973cacf1a7df9ce725c31b14776");
// Get public key.
bc::ec_point public_key = bc::secret_to_public_key(secret);
std::cout << "Public key: " << bc::encode_hex(public_key) << std::endl;
// Create Bitcoin address.
// Normally you can use:
// bc::payment_address payaddr;
// bc::set_public_key(payaddr, public_key);
// const std::string address = payaddr.encoded();
// Compute hash of public key for P2PKH address.
const bc::short_hash hash = bc::bitcoin_short_hash(public_key);
bc::data_chunk unencoded_address;
// Reserve 25 bytes
// [ version:1 ]
// [ hash:20 ]
// [ checksum:4 ]
unencoded_address.reserve(25);
// Version byte, 0 is normal BTC address (P2PKH).
unencoded_address.push_back(0);
// Hash data
bc::extend_data(unencoded_address, hash);
// Checksum is computed by hashing data, and adding 4 bytes from hash.
bc::append_checksum(unencoded_address);
// Finally we must encode the result in Bitcoin's base58 encoding
assert(unencoded_address.size() == 25);
const std::string address = bc::encode_base58(unencoded_address);
std::cout << "Address: " << address << std::endl;
return 0;
}
The code uses a pre-defined private key, so that it produces the same bitcoin address every time it is run:
Example – Compiling and running the addr code
# Compile the addr.cpp code
$ g++ -o addr addr.cpp $(pkg-config --cflags --libs libbitcoin)
# Run the addr executable
$ ./addr
Public key: 0202a406624211f2abbdc68da3df929f938c3399dd79fac1b51b0e4ad1d26a47aa
Address: 1PRTTaJesdNovgne6Ehcdu1fpEdX7913CKKey Formats
Private Key Formats
The private key can be represented in a number of different formats, all of which cor‐ respond to the same 256-bit number. These formats include:
Table – Private Key Representations (Encoding Formats)
| Type | Prefix | Description |
| Hex WIF WIF-compressed |
None 5 K or L |
64 hexadecimal digits Base58Check encoding: Base-58 with version prefix of 128 and 32-bit checksum As above, with added suffix 0x01 before encoding |
The private key we generated earlier can be represented as:
Table – Example: Same Key, Different Formats
| Format | Private Key |
| Hex WIF WIF-compressed |
1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDD 5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2JpbnkeyhfsYB1Jcn KxFC1jmwwCoACiCAWZ3eXa96mBM6tb3TYzGmf6YwgdGWZgawvrtJ |
All of the above representations are different ways of showing the same number, the same private key. They look different, but any one format can easily be converted to any other format.
Decode from Base58Check to Hex
The sx-tools package makes it easy to write shell-scripts and command-line “pipes” that manipulate bitcoin keys, addresses, and transactions. You can use sx-tools to decode the Base58Check format on the command line:
We use the base58check-decode command:
$ sx base58check-decode 5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2JpbnkeyhfsYB1Jcn 1e99423a4ed27608a15a2616a2b0e9e52ced330ac530edcc32c8ffc6a526aedd 128
The result is the hexadecimal key, followed by the Wallet Import Format (WIF) version prefix 128.
Encode from Hex to Base58Check
To encode into Base58Check (the opposite of the previous command), we provide the hex private key, followed by the Wallet Import Format (WIF) version prefix 128:
$ sx base58check-encode 1e99423a4ed27608a15a2616a2b0e9e52ced330ac530edcc32c8ffc6a526aedd 128 5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2JpbnkeyhfsYB1Jcn
Encode from Hex (Compressed Key) to Base58Check encoding
To encode into Base58Check as a “compressed” private key, we add the suffix 01 to the end of the hex key and then encode as above:
$ sx base58check-encode 1e99423a4ed27608a15a2616a2b0e9e52ced330ac530edcc32c8ffc6a526aedd01 128 KxFC1jmwwCoACiCAWZ3eXa96mBM6tb3TYzGmf6YwgdGWZgawvrtJ
The resulting WIF-compressed format, starts with a “K”. This denotes that the private key within has a suffix of “01” and will be used to produce compressed public keys only.
Public Key Formats
Public keys are also presented in different ways, most importantly as either com‐ pressed or uncompressed public keys.
As we saw previously, the public key is a point on the elliptic curve consisting of a pair of coordinates (x,y). It is usually presented with the prefix 04 followed by two 256-bit numbers, one for the x-coordinate of the point, the other for the y-coordinate. The prefix 04 is used to distinguish uncompressed public keys from compressed public keys that begin with a 02 or a 03.
Here’s the public key generated by the private key we created above, shown as the co‐ ordinates x and y.
Public Key K defined as a point K = (x,y).
x = F028892BAD...DC341A y = 07CF33DA18...505BDB
Here’s the same public key shown as a 520-bit number (130 hex digits) with the prefix 04 followed by x and then y coordinates, as 04 x y:
Uncompressed Public Key K shown in hex (130 hex digits) as 04xy.
K = 04F028892BAD...505BDB
Compressed Public Keys
Compressed public keys were introduced to bitcoin to reduce the size of transactions and conserve disk space on nodes that store the bitcoin blockchain database. Most transactions include the public key, required to validate the owner’s credentials and spend the bitcoin. Each public key requires 520 bits (prefix \+ x \+ y), which when multiplied by several hundred transactions per block, or tens of thousands of transac‐ tions per day, adds a significant amount of data to the blockchain.
As we saw in the section “Public Keys” on page 65 above, a public key is a point (x,y) on an elliptic curve. Since the curve expresses a mathematical function, a point on the curve represents a solution to the equation and therefore if we know the x-coordinate we can calculate the y-coordinate by solving the equation y2 mod p = (x3 + 7) mod p. That allows us to store only the x-coordinate of the public key point, omitting the ycoordinate and reducing the size of the key and the space required to store it by 256 bits. An almost 50% reduction in size in every transaction adds up to a lot of data saved over time!
Whereas uncompressed public keys have a prefix of 04, compressed public keys start with either a 02 or a 03 prefix. Let’s look at why there are two possible prefixes: since the left side of the equation is y2 , that means the solution for y is a square root, which can have a positive or negative value. Visually, this means that the resulting y-coordinate can be above the x-axis or below the x-axis. As you can see from the graph of the elliptic curve, the curve is symmetric, meaning it is reflected like a mirror by the x-axis. So, while we can omit the y-coordinate we have to store the sign of y (positive or negative), or in other words we have to remember if it was above or below the x-axis, as each of those options represents a different point and a different public key. When calculating the elliptic curve in binary arithmetic on the finite field of prime order p, the y coordinate is either even or odd, which corresponds to the positive/negative sign as explained above. Therefore, to distinguish between the two possible values of y, we store a com pressed public key with the prefix 02 if the y is even, and 03 if it is odd, allowing the software to correctly deduce the y-coordinate from the x-coordinate and uncompress the public key to the full coordinates of the point.
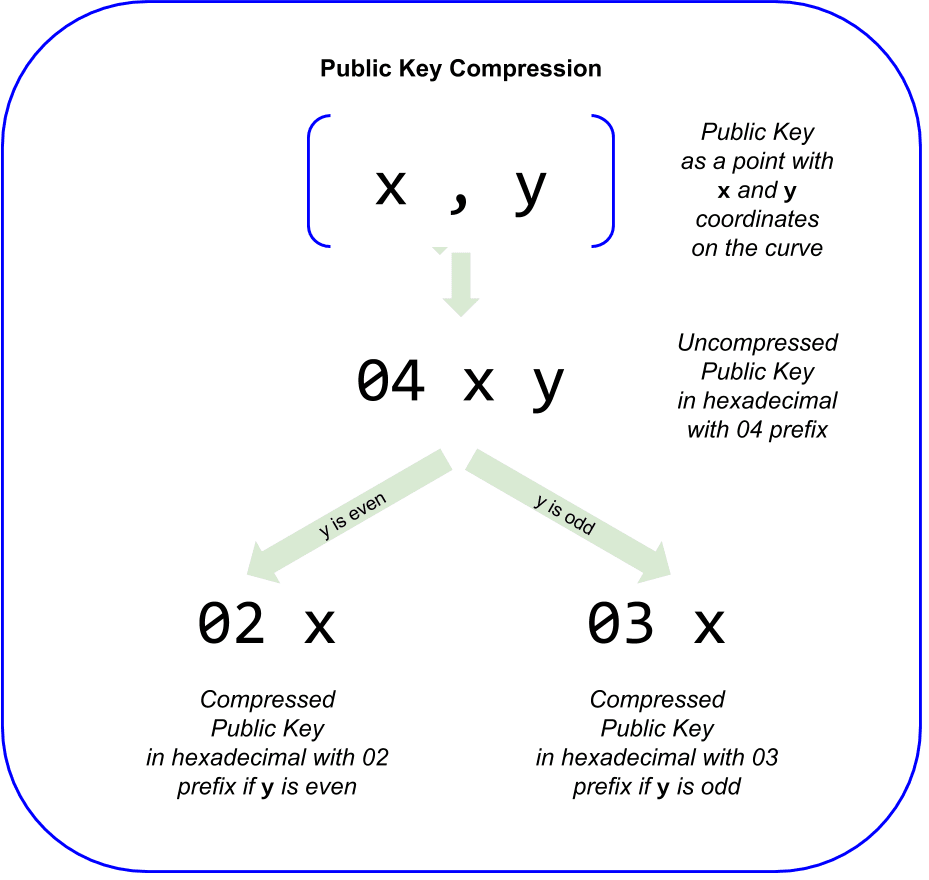
Here’s the same public key generated previously, shown as a compressed public key stored in 264-bits (66 hex digits) with the prefix 03 indicating the y coordinate is odd:
Compressed Public Key K shown in hex (66 hex digits) as K = {02 or 03} x.
K = 03F028892BAD...DC341A
The compressed public key, above, corresponds to the same private key, meaning that it is generated from the same private key. However it looks different from the uncom‐ pressed public key. More importantly, if we convert this compressed public key to a bitcoin address using the double-hash function (RIPEMD160(SHA256(K))) it will produce a different bitcoin address. This can be confusing, because it means that a single private key can produce a public key expressed in two different formats (compressed and uncompressed) which produce two different bitcoin addresses. However, the pri‐ vate key is identical for both bitcoin addresses.
Compressed public keys are gradually becoming the default across bitcoin clients, which is having a significant impact on reducing the size of transactions and therefore the blockchain. However, not all clients support compressed public keys yet. Newer clients that support compressed public keys have to account for transactions from older clients which do not support compressed public keys. This is especially important when a wallet application is importing private keys from another bitcoin wallet application, because the new wallet needs to scan the blockchain to find transactions corresponding to these imported keys. Which bitcoin addresses should the bitcoin wallet scan for? The bitcoin addresses produced by uncompressed public keys, or the bitcoin addresses produced by compressed public keys? Both are valid bitcoin addresses, and can be signed for by the private key, but they are different addresses!
To resolve this issue, when private keys are exported from a wallet, the Wallet Import Format that is used to represent them is implemented differently in newer bitcoin wal‐ lets, to indicate that these private keys have been used to produce compressed public keys and therefore compressed bitcoin addresses. This allows the importing wallet to distinguish between private keys originating from older or newer wallets and search the blockchain for transactions with bitcoin addresses corresponding to the uncompressed, or the compressed public keys respectively. Let’s look at how this works in more detail, in the next section.
Compressed Private Keys
Ironically, the name “compressed private key” is misleading, because when a private key is exported as WIF-compressed it is actually one byte longer than an “uncompressed” private key. That is because it has the added 01 suffix which signifies it comes from a newer wallet and should only be used to produce compressed public keys. Private keys are not compressed and cannot be compressed. The term “compressed private key” really means “private key from which compressed public keys should be derived”, whereas “uncompressed private key” really means “private key from which uncom‐ pressed public keys should be derived”. You should only refer to the export format as “WIF-compressed” or “WIF” and not refer to the private key as “compressed” to avoid further confusion.
Remember, these formats are not used interchangeably. In a newer wallet that imple‐ ments compressed public keys, the private keys will only ever be exported as WIFcompressed (with a K or L prefix). If the wallet is an older implementation and does not use compressed public keys, the private keys will only ever be exported as WIF (5 prefix). The goal here is to signal to the wallet importing these private keys whether it must search the blockchain for compressed or uncompressed public keys and addresses.
If a bitcoin wallet is able to implement compressed public keys, then it will use those in all transactions. The private keys in the wallet will be used to derive the public key points on the curve, which will be compressed. The compressed public keys will be used to produce bitcoin addresses and those will be used in transactions. When exporting pri‐ vate keys from a new wallet that implements compressed public keys, the Wallet Import Format is modified, with the addition of a one-byte suffix +01+to the private key. The resulting base58check encoded private key is called a “Compressed WIF” and starts with the letter K or L, instead of starting with “5” as is the case with WIF encoded (noncompressed) keys from older wallets.
Here’s the same key, encoded in WIF and WIF-compressed formats
Table – Example: Same Key, Different Formats
| Format | Private Key |
| Hex WIF Hex-compressed WIF-compressed |
1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDD 5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2JpbnkeyhfsYB1Jcn 1E99423A4ED27608A15A2616A2B0E9E52CED330AC530EDCC32C8FFC6A526AEDD_01_ KxFC1jmwwCoACiCAWZ3eXa96mBM6tb3TYzGmf6YwgdGWZgawvrtJ |
“Compressed private keys” is a misnomer! They are not com‐ pressed, rather the WIF-compressed format signifies that they should only be used to derive compressed public keys and their correspond‐ ing bitcoin addresses. Ironically, a “WIF-compressed” encoded pri‐ vate key is one byte longer because it has the added 01 suffix to dis‐ tinguish it from an “uncompressed” one.
This article has been published from the source link without modifications to the text. Only the headline has been changed.