Learn the most important Basics of Deep Learning and Neural Networks in this detailed Tutorial.
This is a beginner’s guide to Deep Learning and Neural networks. In the following article, we are going to discuss the meaning of Deep Learning and Neural Networks. In particular, we will focus on how Deep Learning works in practice.
Table of Content
- What exactly is Deep Learning?
- Why is Deep Learning so popular these Days?
- Biological Neural Networks
- Artificial Neural Networks
- Neural Network Architecture
- Layer Connections
- Learning Process in a Neural Network
- Loss Functions
- Gradient Descent
Have you ever wondered how Google’s translator App is able to translate entire paragraphs from one language into another in a matter of milliseconds?
How Netflix and YouTube are able to figure out our taste in movies or videos and give us appropriate recommendations?
Or how self-driving cars are even possible?
All of this is a product of Deep Learning and Artificial Neural Networks. The definition of Deep Learning and Neural networks will be addressed in the following.
Lets us begin with the definition of Deep Learning first.
1. What exactly is Deep Learning?
Deep Learning is a subset of Machine Learning, which on the other hand is a subset of Artificial Intelligence. Artificial Intelligence is a general term that refers to techniques that enable computers to mimic human behavior. Machine Learning represents a set of algorithms trained on data that make all of this possible.
Deep Learning, on the other hand, is just a type of Machine Learning, inspired by the structure of a human brain. Deep learning algorithms attempt to draw similar conclusions as humans would by continually analyzing data with a given logical structure. To achieve this, deep learning uses a multi-layered structure of algorithms called neural networks.
The design of the neural network is based on the structure of the human brain. Just as we use our brains to identify patterns and classify different types of information, neural networks can be taught to perform the same tasks on data.
The individual layers of neural networks can also be thought of as a sort of filter that works from gross to subtle, increasing the likelihood of detecting and outputting a correct result.
The human brain works similarly. Whenever we receive new information, the brain tries to compare it with known objects. The same concept is also used by deep neural networks.
Neural networks enable us to perform many tasks, such as clustering, classification or regression. With neural networks, we can group or sort unlabeled data according to similarities among the samples in this data. Or in the case of classification, we can train the network on a labeled dataset in order to classify the samples in this dataset into different categories.
In general, neural networks can perform the same tasks as classical algorithms of machine learning. However, it is not the other way around.
Artificial neural networks have unique capabilities that enable deep learning models to solve tasks that machine learning models can never solve.
All recent advances in artificial intelligence in recent years are due to deep learning. Without deep learning, we would not have self-driving cars, chatbots or personal assistants like Alexa and Siri. The Google Translate app would continue to be as primitive as 10 years ago (before Google switched to neural networks for this App), and Netflix or Youtube would have no idea which movies or TV series we like or dislike. Behind all these technologies are neural networks.
We can even go so far as to say that today a new industrial revolution is taking place, driven by artificial neural networks and deep learning.
At the end of the day, deep learning is the best and most obvious approach to real machine intelligence we’ve had so far.
2. Why is Deep Learning is Popular these Days?
Why is deep learning and artificial neural networks so powerful and unique in today’s industry? And above all, why are deep learning models more powerful than machine learning models? Let me explain it to you.
The first advantage of deep learning over machine learning is the needlessness of the so-called feature extraction.
Long before deep learning was used, traditional machine learning methods were mainly used. Such as Decision Trees, SVM, Naïve Bayes Classifier and Logistic Regression.
These algorithms are also called flat algorithms. Flat here means that these algorithms can not normally be applied directly to the raw data (such as .csv, images, text, etc.). We need a preprocessing step called Feature Extraction.
The result of Feature Extraction is a representation of the given raw data that can now be used by these classic machine learning algorithms to perform a task. For example, the classification of the data into several categories or classes.
Feature Extraction is usually quite complex and requires detailed knowledge of the problem domain. This preprocessing layer must be adapted, tested and refined over several iterations for optimal results.
On the other side are the artificial neural networks of Deep Learning. These do not need the Feature Extraction step.
The layers are able to learn an implicit representation of the raw data directly and on their own. Here, a more and more abstract and compressed representation of the raw data is produced over several layers of an artificial neural-nets. This compressed representation of the input data is then used to produce the result. The result can be, for example, the classification of the input data into different classes.
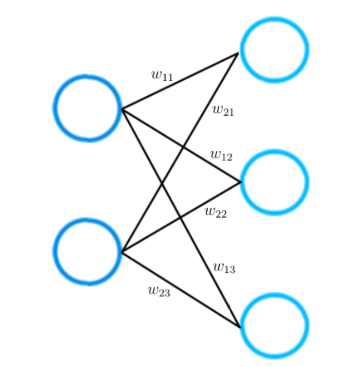
As mentioned earlier: each connection between two neurons is represented by a numerical value, which we call weight.
As you can see in the picture, each connection between two neurons is represented by a different weight w. Each of these weight w has indices. The first value of the indices stands for the number of neurons in the layer from which the connection originates, the second value for the number of the neurons in the layer to which the connection leads.
All weights between two neural network layers can be represented by a matrix called the weight matrix.
A weight matrix.A weight matrix has the same number of entries as there are connections between neurons. The dimensions of a weight matrix result from the sizes of the two layers that are connected by this weight matrix.
The number of rows corresponds to the number of neurons in the layer from which the connections originate and the number of columns corresponds to the number of neurons in the layer to which the connections lead.
In this particular example, the number of rows of the weight matrix corresponds to the size of the input layer which is two and the number of columns to the size of the output layer which is three.
7. Learning Process of a Neural Network
Now that we understand the neural network architecture better, we can intuitively study the learning process. Let us do it step by step. The first step is already known to you.
For a given input feature vector x, the neural network calculates a prediction vector, which we call here as h.
Forward Propagation.This step is also referred to as the forward propagation. With the input vector x and the weight matrix W connecting the two neuron layers, we compute the dot product between the vector x and the matrix W.
The result of this dot product is again a vector, which we call
Equations for Forward Propagation.z. The final prediction vector h is obtained by applying a so-called activation function to the vector z. In this case, the activation function is represented by the letter Sigma. An activation function is only a nonlinear function that performs a nonlinear mapping from z to h.
There are 3 activation functions that are used in Deep Learning, which are tanh, sigmoid, and ReLu.
At this point, you may recognize the meaning behind neurons in a neural network. A neuron is simply a representation of a numeric value.
Let’s take a closer look at vector z for a moment. As you can see, each element of z consists of the input vector x. At this point, the role of the weights unfolds beautifully. A value of a neuron in a layer consists of a linear combination of neuron values of the previous layer weighted by some numeric values.
These numerical values are the weights that tell us how strongly these neurons are connected with each other.
During training, these weights are adjusted, some neurons become more connected, some neurons become less connected. As in a biological neural network, learning means the alteration of weights. Accordingly, the values of z, h and the final output vector y are changing with the weights. Some weights make the predictions of a neural network us closer to the actual ground truth vector y_hat, some weights increase the distance to the ground truth vector.
Now that we know how the mathematical calculations between two neural network layers look like, we can extend our knowledge to a deeper architecture that consists of 5 layers.
Same as before we calculate the dot product between the input x and the first weight matrix W1 and apply an activation function to the resulting vector to obtain the first hidden vector h1. h1 is now considered as the input for the upcoming third layer. The whole procedure from before is repeated until we obtain the final output y:
Equations for Forward PropagationYou still here?? Nice!!
8. Loss Functions
After we get the prediction of the neural network, in the second step we must compare this prediction vector to the actual ground truth label. We call the ground truth label as vector y_hat.
While the vector y contains the predictions that the neural network has computed during the forward propagation (and which may, in fact, be very different from the actual values), the vector y_hat contains the actual values.
Mathematically, we can measure the difference between y and y_hat by defining a loss function which value depends on this difference.
An example of a general loss function is the quadratic loss:
The value of this loss function depends on the difference between y_hat and y. A higher difference means a higher loss value, a smaller difference means a smaller loss value.
Minimizing the loss function directly leads to more accurate predictions of the neural network, as the difference between the prediction and the label decreases.
Minimizing the loss function automatically causes the neural network model to make better predictions regardless of the exact characteristics of the task at hand. You only have to select the right loss function for the task. Fortunately, there are only two loss functions that you should know about to solve almost any problem that you encounter in practice.
These loss-functions are the Cross-Entropy Loss:
and the Mean Squared Error Loss:
Since the loss depends on the weights, we must find a certain set of weights for which the value of the loss function is as small as possible. The method of minimizing the loss function is achieved mathematically by a method called gradient descent
9. Gradient Descent
During gradient descent, we use the gradient of a loss function (or in other words the derivative of the loss function) to improve the weights of a neural network.
To understand the basic concept of the gradient descent process, let us consider a very basic example of a neural network consisting of only one input and one output neuron connected by a weight value w.
This neural network receives an input x and outputs a prediction y. Let say the initial weight value of this neural network is 5 and the input x is 2. Therefore the prediction y of this network has a value of 10, while the label y_hat might have a value of 6.
This means that the prediction is not accurate and we must use the gradient descent method to find a new weight value that causes the neural network to make the correct prediction. In the first step, we must choose a loss function for the task. Let’s take the quadratic loss that I have defined earlier and plot this function, which basically is just a quadratic function:
The y-axis is the loss value which depends on the difference between the label and the prediction, and thus the network parameters, in this case, the one weight w. The x-axis represents the values for this weight. As you can see there is a certain weight w for which the loss function reaches a global minimum. This value is the optimal weight parameter that would cause the neural network to make the correct prediction which is 6. In this case, the value for the optimal weight would be 3:
Our initial weight, on the other hand, is 5, which leads to a fairly high loss. The goal now is to repeatedly update the weight parameter until we reach the optimal value for that particular weight. This is the time when we need to use the gradient of the loss function. Fortunately, in this case, the loss function is a function of one single variable, which is the weight w:
In the next step, we calculate the derivative of the loss function with respect to this parameter:
In the end, we get a result of 8, which gives us the value of the slope or the tangent of the loss function for the corresponding point on the x-axis at which our initial weight lies.
This tangent points towards the highest rate of increase of the loss function and the corresponding weight parameters on the x-axis.
This means that we have just used the gradient of the loss function to find out which weight parameters would result in an even higher loss value. But what we want to know is the exact opposite. We can get what we want, if we multiply the gradient by minus 1 and this way obtain the opposite direction of the gradient. This way we get the direction of the highest rate of decrease of the loss function and the corresponding parameters on the x-axis that cause this decrease:
In the final step, we perform one gradient descent step as an attempt to improve our wights. We use this negative gradient to update your current weight in the direction of the weights for which the value of the loss function decreases according to the negative gradient:
Gradient Descent Step. Gradient Descent Step.The factor epsilon in this equation is a hyperparameter called the learning rate. The learning rate determines how quickly or how slowly you want to update the parameters. Please keep in mind that the learning rate is the factor with which we have to multiply the negative gradient and that the learning rate is usually quite small. In our case, the learning rate is 0.1.
As you can see, our weight w after the gradient descent is now 4.2 and closer to the optimal weight than it was before the gradient step.
New Weights after Gradient Descent.The value of the loss function for the new weight value is also smaller, which means that the neural network is now capable to do a better prediction. You can do the calculation in your head and see that the new prediction is, in fact, closer to the label than before.
Each time we are performing the update of the weights, we move down the negative gradient towards the optimal weights.
After each gradient descent step or weight update, the current weights of the network get closer and closer to the optimal weights until we eventually reach them and the neural network will be capable to do the predictions we want to make.
This article has been published from the source link without modifications to the text. Only the headline has been changed.